Расписание

Cтраница 1

Расписания, определяемые перестановками л ( 2, 4, 5, 6 1, 3) и я ( 2, 4, 5, 6, 3 1), являются оптимальными. [1]

Расписание s на интервале ( т), rj б ], где 1 ] 0, строится следующим образом. [2]

Расписание s в задаче 1.1, в) однозначно определяется парой перестановок п ( 1) и я ( 2), задающих порядок обслуживания требований множества N каждым из приборов. [3]

Расписание должно быть вывешено в подразделении на видном месте для ознакомления слушателей и вручено всем преподавателям не позднее чем за 3 дня до начала занятий. [4]

Расписание для задачи об утечке нефти работает следующим образом ( см. разд. Из расписания выбирается задача. Она объявляется текущей задачей и просматриваются все правила, чтобы выяснить, можно ли ( и каким образом) их применить. Метаправила разрушают любые связи между имеющимися правилами, и эти правила затем выполняются в очередности одно за другим. Суть в том, что, хотя некоторые правила лучше, чем другие, много правил лучше, чем одно. Только после того, как пройдет некоторое время, RLL сделает паузу и посмотрит, была ли выполнена ( и как) задача. Часто в процессе решения задачи какое-то правило добавляет к расписанию одну или несколько новых задач. У каждой задачи есть список символов, обозначающих причины, по которым она была включена в расписание; этот список позволяет вычислить численное значение приоритета. Таким образом, некоторые новые задачи могут быть помещены в расписание работ с высоким приоритетом, а другие - с очень низким. Хотя обработку расписания следует определять в самом начале, для получения процессора задач можно скопировать процессор правил и осуществить тривиальное его редактирование. Эта отредактированная копия в свою очередь снова может быть отредактирована, с тем чтобы получить, наконец, процессор расписания. [5]

Расписание без прерываний занимает 4 единицы времени. [6]

Расписание, приведенное на рис. 2.2, иллюстрирует важное свойство расписаний минимальной длины без прерываний. [7]

Расписание, показанное на рис. 2.2, б, представляет собой списочное расписание для системы заданий, изображенной на рис. 2.2, а, в котором список упорядочен по убыванию меток. Поэтому задание 11, следующее по списку после задания 12, назначается на третий процессор. [8]

Расписание для леса ( / -, ) может быть получено путем добавления фиктивного задания, являющегося непосредственным преемником всех конечных вершин ( Jr, ), и последующего применения пунктов 1 - 3 к новой системе заданий. [9]

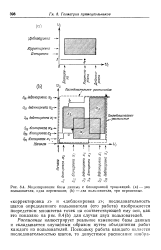Моделирование базы данных с блокировкой транзакций, ( а-два пользователя, одна переменная. ( Ь - два пользователя, три переменные. [10]

Расписание иллюстрирует реальное изменение базы данных и складывается случайным образом путем объединения работ каждого из пользователей. [11]

Расписание для параллельно работающих, операторов. Более того, некоторые работы не могут выполняться, пока не кончены другие: существует строго верхняя треугольная матрица р ( pij), такая, что р - / - 1, если работа i должна быть выполнена перед работой Д р / у 1, если работа / должна быть выполнена перед работой i, и р у 0, если работы выполняются независимо друг от друга. [12]

Расписание еще более помогает организации учебного процесса, когда составляется с учетом пожеланий студентов. К тому же студенты не имеют достаточного представления о характере, назначении, взаимозащсимости: и степени сложности дисциплин, что не позволяет им наметить расписание занятий с необходимой обоснованностью. [13]

РЕЙСЫ ( расписание авиалинии. [14]

Расписание в табл. 1.1 представляет собой пример отношения типа РЕЙСЫ. Эти метки называются именами атрибутов. Каждому имени атрибута ставится в соответствие множество допустимых для соответствующего столбца значений. Это множество называется доменом данного имени атрибута. [15]

Страницы: 1 2 3 4