Расположение - отклонение
Cтраница 3
Отклонением расположения поверхности или профиля называют отклонение реального расположения поверхности ( профиля) от его номинального расположения. Количественно отклонения расположения оценивают в соответствии с определениями, приведенными ниже. При оценке отклонений расположения отклонения формы рассматриваемых поверхностей ( профилей) и базовых элементов ( обобщенный термин, под которым понимают поверхность, линию или точку) должны быть исключены из рассмотрения. При этом реальные поверхности ( профили) заменяют прилегающими, а за оси, плоскости симметрии и центры реальных поверхностей ( профилей) принимают оси, плоскости симметрии и центры прилегающих элементов. [31]
 |
Отклонения формы плоских поверхностей. [32] |
Отклонением расположения поверхности или профиля называют отклонение реального расположения поверхности ( профиля) от его номинального расположения. Количественно отклонения расположения оцениваются в соответствии с определениями, приведенными ниже. При оценке отклонений расположения отклонения формы рассматриваемых поверхностей ( профилей) и базовых элементов должны исключаться из рассмотрения. При этом реальные поверхности ( профили) заменяются прилегающими, а за оси, плоскости симметрии и центры реальных поверхностей ( профилей) принимают оси, плоскости симметрии и центры прилегающих элементов. [33]
 |
Отклонение формы заданного профиля. [34] |
Отклонением расположения поверхности или профиля называют отклонение реального расположения поверхности ( профиля) от его номинального расположения. Количественно отклонения расположения оценивают в соответствии с определениями, приведенными ниже. При оценке отклонений расположения отклонения формы рассматриваемых поверхностей ( профилен) и базовых элементов ( обобщенный термин, под которым понимают поверхность, линию или точку) должны быть исключены из рассмотрения. При этом реальные поверхности ( профили) заменяют прилегающими, а за осп, плоскости симметрии и центры реальных поверхностей ( профилей) принимают оси, плоскости симметрии и центры прилегающих элементов. [35]
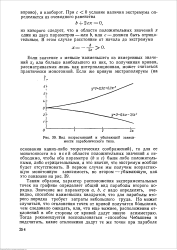 |
Вид возрастающей и убывающей зависимости параболического типа. [36] |
Таким образом, характер расположения экспериментальных точек на графике определяет общий вид параболы второго порядка. Значение же параметров а, Ъ, с надо определять, очевидно, способом наименьших квадратов, что для параболы второго порядка требует затраты небольшого труда. Но может случиться, что отклонения точек от кривой получатся большими, чем следовало ожидать, или, что еще важнее, расположения отклонений в обе стороны от кривой дадут явную асимметрию. [37]
Измерение отклонений взаимного расположения поверхностей предполагает, что одна из поверхностей или ее геометрическая ось принимаются за базу. Отсчет отклонений расположения производится относительно базы. Аналогично определяются значения суммарных отклонений формы и расположения. При определении значений отклонений расположения отклонения формы базовой и исследуемой поверхностей должны исключаться. Это делается заменой реальных поверхностей прилегающими. Прилегающие поверхности при измерении могут имитироваться элементами приспособлений или приборов. Однако в этом случае высокая точность измерения не обеспечивается. Большинство используемых схем измерения или совпадает с представленными выше, или построено на их основе. [38]
Но вводить в оценку среднего эту маловероятную возможность его ошибочности мы не умеем, а поэтому должны просто решить, выбросить эту цифру или оставить. Для такого решения нужны какие-то более или менее ( надежные критерии. Подобные критерии в литературе имеются. Однако прежде чем перейти к их изложению, полезно напомнить, что существует такой центр совокупности, который а в том этически исключает все выскакивающие как слишком малые, так и слишком большие цифры. Таким центром является хорошо известная нам медиана, использование которой необязательно связано с асимметричностью отклонений и которую мы вправе применять даже в тех случаях, когда генеральная совокупность наверное обладает симметрией. Но симметричность выборки вообще не очень обязательна, в отдельных случаях она может сильно нарушиться из-за присутствия хотя бы одной выскакивающей цифры. Во всяком случае, переход от среднего арифметического к медиане может сильно помочь при оценке среднего. Вопрос же о предпочтительности медианы при асимметричном, по существу, расположении отклонений будет рассмотрен в дальнейшем вне зависимости от наличия выскакивающих ошибок. Однако заранее ясно, что положительные свойства медианы скажутся и в этом отношении. [39]
Страницы: 1 2 3