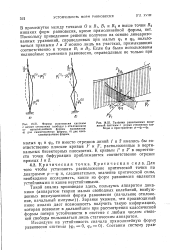
Расположение - критическая точка
Cтраница 2
Фазовое состояние пластовой смеси и особенности их фазового поведения при разработке месторождений определяются пластовыми давлениями и температурами, а также составом смеси, от которого зависит ширина петли и расположение критической точки, точек максимального давления к максимальной температуры. [16]
 |
Тройные диаграммы смесей. [17] |
Критические кривые изученных тройных смесей при С 0 5 имеют такой же вид, что и критические кривые бинарных смесей метана с парафиновыми углеводородами, и их положение на графике вполне соответствует расположению критических точек бинарных смесей, состоящих из бензола и парафинового углеводорода. [18]
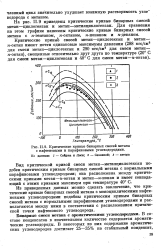 |
Критические кривые бинарных смесей метана с нафтеновыми и парафиновыми углеводородами. [19] |
Из приведенных данных можно сделать заключение, что критические кривые бинарных смесей метана с моноциклическими нафтеновыми углеводородами подобны критическим кривым бинарных смесей метана с нормальными парафиновыми углеводородами и располагаются между ними в соответствии с расположением критической точки нафтенового углеводорода. [20]
Рассмотрим более детально этот вопрос. Из расположения критических точек смесей на пограничных кривых до и после критической точки азеотропа ( вдоль критической кривой) видно, что направления критических изобар - изотерм в критической точке азеотропа изменяются. В этой точке скачком происходит переход от минимального критического давления к максимальному. Если двигаться вдоль критической кривой со стороны компонента с молекулами меньшего объема, производные ( dv / dN2) p T K в критических точках смесей будут положительными. Если же двигаться к этой критической точке азеотропа со стороны двойной критической точки ( меньшие температуры), то в этом случае ( dvjdN p, т, к, аз - - - Поэтому в критической точке азеотропа на изобаре - изотерме v - N2 не может быть точки перегиба с вертикальной касательной. На этом рис. представлены экспериментальные данные для системы этан - двуокись углерода. Показаны три изотермы равновесия с критическими точками. Для каждой из них построены критические изобары - изотермы. [21]
Расположение критических точек на концах щели приводит к тому, что в потоке отсутствуют бесконечные скорости. Высказанное предположение о расположении критических точек аналогично гипотезе Жуковского о расположении критической точки течения на задней кромке крылового профиля ( см. гл. [22]
Для того чтобы установить расположение критической точки на диаграмме р - ф и, следовательно, значение критической силы, необходимо исследовать, какие из форм равновесия являются устойчивыми и какие неустойчивыми. [24]
Расположение критических точек на концах щели приводит к тому, что в потоке отсутствуют бесконечные скорости. Высказанное предположение о расположении критических точек аналогично гипотезе Жуковского о расположении критической точки течения на задней кромке крылового профиля ( см. гл. [25]
Характер кривых кинетики сушки зависит от формы связи влаги с материалом. Изменение режима сушки не может привести к изменению характера кривых кинетики сушки, а только ганосит изменения в расположение критических точек. [26]
Если при некоторых значениях параметров это удается сделать, то процедуру можно повторять многократно, получая последовательность операторов эволюции для все больших и больших временных интервалов. Процедура перехода от старого оператора к новому, перенормированному, называется РГ преобразованием, а набор значений параметров, о котором мы говорили, задает расположение критической точки. В критической точке структура операторов эволюции на больших временах оказывается обусловленной не конкретным видом исходного оператора системы, а структурой РГ преобразования. В этом и состоит универсальность. Поскольку в критической точке получаемые при многократном применении РГ преобразования операторы эволюции оказываются одинаковыми с точностью до масштабной замены переменных, система должна демонстрировать на различных временах подобную динамику с соответствующим пересчетом масштаба динамических переменных, проявляя свойство скейлинга. [27]
Следовательно, угол а определяется направлением скорости набегающего потока и направлением бесциркуляционного обтекания профиля. Этот угол часто называют теоретическим углом атаки. Если профиль не имеет острой задней кромки, то постулат Жуковского-Чаплыгина может быть использован только при дополнительном допущении о расположении задней критической точки. [28]
Страницы: 1 2