Расположение - ненулевой элемент
Cтраница 1
Расположение ненулевых элементов сохраняется для данной конфигурации сети и не зависит от расчетного времени и параметров газотранспортной сети. [1]
Расположение ненулевых элементов носит характер симметричного относительно главной диагонали, если в качестве неизвестных функций приняты функции квадрата давления в узлах, и зависит от нумерации узлов. [2]
Важной особенностью матриц Н, Q является сохранение ими специфики расположения ненулевых элементов матрицы Y. При этом необходимо, чтобы любая вертикальная ( горизонтальная) прямая линия имела с правой ( левой) частью границы, выделяющей в матрице Y нулевые элементы ( рис. 8.9, а), односвязаное множество общих точек. Математически это условие записывается следующим образом. [3]
При построении динамических моделей экономики, да и в других областях-возникают матрицы, расположение ненулевых элементов которых изображено на рис. 6.12. В общем случае такую матрицу А [ М, N ] можно описать следующим образом. [4]
Многие приложения приводят к матрицам, которые не только разрежены, но и имеют особую структуру расположения ненулевых элементов. Такие матрицы называются трехдиагональными. [6]
Объединяя (5.17) - (5.19), легко видеть, что построенная нами по методу Ритца вариационно-разностная схема по структуре расположения ненулевых элементов и их виду практически совпадает с чисто разностными схемами. В частности, для случая постоянных р ( х, у) и q ( x, у) вариационно-разностный и разностный аналоги дифференциального оператора полностью совпадают. Отмеченное обстоятельство позволит применять для решения системы (5.17) эффективные итерационные методы, такие как метод расщепления, последовательной верхней релаксации и другие. [7]
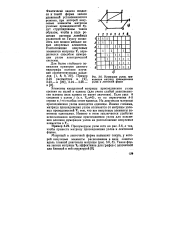 |
Нумерация узлов, приводящая матрицу присоединения узлов к ленточной форме. [8] |
Фактически задача сводится к такой форме записи уравнений установившегося режима, при которой ненулевые элементы матрицы узловых проводимостей будут сгруппированы таким образом, чтобы в ходе решения системы линейных уравнений по Гауссу появилось как можно меньше новых ненулевых элементов. Расположение ненулевых элементов матрицы Yy определяется способом нумерации узлов электрической системы. [9]
Задача (4.52) так же, как и задача (4.26) - ( 4: 27), может быть. Однако большая разреженность и наличие закономерностей в расположении ненулевых элементов остаются. Кроме того, матрица ограничений (4.52) имеет полный ранг, и рассмотренный в гл. [10]
Проведение доказательства для каждого конкретного случая обычно выявляет эти функции с точностью до постоянного множителя. Таким образом, в методе Галеркина отыскиваются не только веса в разложении гладкой составляющей по базисным функциям метода конечных элементов, но и веса особых функций. Основная трудность применения этого метода состоит в том, что функции wt усложняют структуру расположения ненулевых элементов алгебраической системы, так как носители этих функций захватывают большое количество элементарных областей. [11]
При отсутствии перестановок сохраняется ширина ленты. Внутри ленты может происходить заполнение. Для больших разреженных матрице нетипичным расположением ненулевых элементов может потребоваться специальная структура данных. [12]
Если при этом в (9.5) осуществляется, как и в (4.11), точное интегрирование ( или, скажем, численное интегрирование по методу Гаусса достаточно высокого порядка), то получаемая таким путем матрица те ( соответственно и матрица М) называется согласованной. Данный термин подчеркивает, согласованность формулировок жесткостных и массовых характеристик конечноэлементной модели. В случае согласованной формулировки матрица М имеет такую же структуру, что и К. В частности, обе матрицы имеют одинаковое расположение ненулевых элементов и требуют одинакового объема памяти ЭВМ для своего хранения. [13]
На практике были решены линейные системы со 100 тысячами неизвестных. Матрица такой системы состоит из 1010 элементов, и, если бы она была полной, ее невозможно было бы поместить в память существующих вычислительных систем, не говоря уже о реализации самого процесса решения уравнений. Существуют решенные задачи линейного программирования с 1 миллионом неравенств и 50 тысячами неизвестных. Матрица такой задачи состоит из 5 1010 элементов, которые почти все должны быть нулевыми, чтобы задача могла быть решена. На рис. 4.1 показан пример расположения ненулевых элементов в двух больших разреженных матрицах, полученных из реальных приложений. [14]
Возможность такой минимизации заложена в самой структуре прямых методов. Каждый из них допускает выбор для проведения очередного шага любого из еще не обработанных столбцов и ( или) любой из оставшихся строк. Каждому такому выбору соответствует свое значение последующего заполнения. Как оказывается, можно заранее промоделировать весь процесс решения системы в целочисленной или булевой арифметике и выбрать оптимальный в том или ином смысле порядок строк и столбцов. Эта, вообще говоря довольно значительная, предварительная работа вполне оправданна, если решается целый класс задач с одинаковым расположением ненулевых элементов. [15]
Страницы: 1 2
