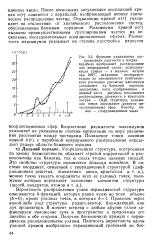
Хаотическое расположение - частица
Cтраница 1
 |
Модель высокопористого монодисперсного материала, по которой определяется его эффективная теплопроводность. [1] |
Хаотическое расположение частиц ( рис. 6 - 1, а) заменяем упорядоченным ( рис. 6 - 1, б), при котором расстояние / между частицами в направлении теплового потока q принимаем по формуле ( 6 - 2), а наличие контактов заменим моделью твердых бесконечно тонких стержней, соединяющих частицы. [2]
Аналогичное выражение приведено в работе [139] для хаотического расположения частиц с учетом градиентов средних скоростей и объемной концентрации вдоль направления движения. [3]
Таммана, рассматривавшего стекло, как переохлажденную жидкость с абсолютно хаотическим расположением частиц. При низкой температуре вязкость стекла так сильно увеличивается, что сообщает ему видимую неподвижность - твердость в механическом смысле. Стекло, таким образом, приобретает некоторые свойства истиннотвердых веществ, как, например, хрупкость. Но, в основном, стекло и при низкой температуре остается веществом аморфноподобным, отличающимся от кристалла отсутствием правильной ориентировки молекул ( пространственной решетки), физической анизотропности и определенных точек плавления. [4]
Старение сопровождается структурными изменениями в веществе дисперсной фазы ( у лиофобных золей-в ядрах мицелл): сменой хаотического расположения частиц, все более ориентированным их расположением, кончающимся для лиофобных золей построением общих кристаллических решеток и потерей связи между дисперсной и дисперсионной фазами. [5]
Воюцкому, старение геля - это переход системы из неравновесного состояния в равновесное. Хаотическое расположение частиц заменяется ориентированным, число контактов между частицами возрастает вследствие их стремления занять такое взаимное положение, при котором потенциальная энергия системы минимальна. [6]
При хаотическом расположении частиц плиты могут считаться изотропными в их плоскости. Для увеличения прочности плит частицам древесины придается определенная ориентация - или общая для всей плиты, или разная в разных слоях. Плиты с ориентированными древесными частицами могут быть отнесены к квазигомогенным ортотропным материалам при условии, что размеры частиц малы по сравнению с размерами изделия, а технология обеспечивает однородность свойств по всему объему слоя. [7]
После нескольких затухающих осцилляции кривая 0 ( г) сливается с параболой, изображающей вполне хаотическое распределение частиц. Осцилляции кривой о ( г) указывают на отклонения от хаотического расположения частиц, обусловленные ближним порядком. Максимумы кривой о ( г) вызваны преимущественными группировками частиц на нескольких последовательных координационных сферах. [9]
Под старением понимают всю сумму процессов, происходящих в коагулянтах ( агрегатах гидроокисей) после их образования. Это переход из неравновесного состояния в равновесное, в ходе которого хаотическое расположение частиц заменяется ориентированным, число контактов между частицами возрастает ввиду их стремления к такому взаимному расположению, при котором потенциальная энергия минимальна. [10]
Всю сумму процессов, происходящих в коагулятах после их образования, часто объединяют общим термином старение. Так или иначе в результате старения, независимо от того, происходит ли кристаллизация или нет, хаотическое расположение частиц в агрегатах заменяется ориентированным, число контактов между частицами возрастает вследствие их стремления занять такое взаимное положение, при котором потенциальная энергия системы1 - минимальна [ 149 ( стр. [11]
Метод основан на обнаруженной нами способности частиц кокса, взвешенных в диэлектрической жидкости, ориентироваться под действием переменного электрического поля высокой напряженности. Анизотропность коксов определяют по отношению тангенса диэлектрических потерь смеси кокса и диэлектрической жидкости после ориентирования частиц в электрическом поле к to смеск при хаотическом расположении частиц. [12]
Значение константы k в формуле (2.20) может быть различным в зависимости от особенностей метода решения, взаимного расположения частиц в суспензии и от того, учитывается или нет отсутствие скольжения жидкости на стенках канала. Значения k, полученные различными исследователями, лежат в пределах от 1 3 для хаотически распределенных частиц до 1 9 для кубической решетки. Хаотическое расположение частиц в суспензии, исследованное в работе [104], создавалось с использованием программы, генерирующей случайные числа. [13]
Формула ( 12), предполагаемая для использования на всем диапазоне рабочих индукций, получена на основе измерений угла а на моделях наполнителя, а также на предположении расположения частиц в виде правильных структур. В результате имеют место погрешности от недоучета на моделях наполнителя мо-лекулярно-механических связей между частицами, а также несоответствия действительному хаотическому расположению частиц. [14]
Теорию опалесценции проще всего построить, рассчитав рассеяние света от одной частицы и перенеся затем полученный результат на совокупность частиц. В простейшем случае рассматривается рассеяние света сферическими частицами, так как только при полной симметрии их формы рассеяние не зависит от положения частицы по отношению к плоскости, образуемой падающим лучом и направлением наблюдения. Если частица имеет анизометрическую форму, то необходимо учитывать зависимость рассеяния от ориентации частицы по отношению к указанной плоскости. При совершенно хаотическом расположении частиц все ориентации их равновероятны, что приводит к усреднению, и рассеяние света вновь подчиняется формуле для частиц сферической формы ( при достаточно малых размерах) с некоторым эффективным радиусом. Если по каким-либо причинам анизометрические частицы ориентированы, то формула, описывающая среднее рассеяние от одной частицы, соответствует форме и ориентации частицы в случае полной ориентации или какой-то эффективной форме в случае частичной ориентации. [15]
Страницы: 1