Взаимное расположение - область
Cтраница 1
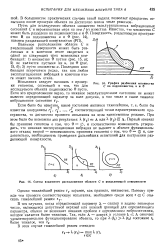 |
Схемы взаимного расположения области С и разделяющей поверхности. [1] |
Взаимное расположение области С и разделяющей поверхности может быть различным и в конечном итоге сводиться к одной из следующих трех возможных комбинаций: 1) множество и пустое ( рис. 15, а); 2) не являются пустыми ни и, ни О ( рис. 15, б); 3) пусто множество и. Последняя комбинация встречается редко, так как любая эксплуатационная вибрация в конечном итоге может вызвать отказ. [2]
Взаимное расположение области G и кривой / может быть произвольным. [3]
Взаимное расположение области Q и кривой С может быть совершенно произвольно. [4]
Существуют два варианта взаимного расположения областей переполнения Н и основной. [5]
Используемая процедура оптимизации предусмагривает анализ взаимного расположения областей пространства оптимизируемых параметров, определяемых допустимыми значениями критериев. Поскольку возможна несовместность допустимых областей, то не исключается корректировка исходных данных. Кроме этого, различное расположение названных областей предполагает использование соответствующих численных методов при поиске оптимума. [6]
Если известна полная информация о характере взаимного расположения областей v и заданы феноменологические модели фаз, то говорят, что построена модель кусочно-однородной ( композиционной) среды. [7]
С этой целью откажемся от учета взаимного расположения областей только пары классов, так как это приводит к максимальному числу решаемых дихотомических задач. При любом другом способе решения задачи распознавания с ростом числа распознаваемых классов также наблюдается увеличение числа разделяющих поверхностей. [8]
Бели известна полная информация о характере взаимного расположения областей Uk и заданы феноменологические модели фаз, то говорят, что построена модель кусочно-однородной ( композиционной) среды. [9]
Подобным образом достаточно точно удается определить границы и взаимное расположение областей ректификации, необходимые при выборе схем разделения многокомпонентных неидеальных смесей. [10]
На рис. 8 - 4 приведены различные случаи взаимного расположения областей S и Т и отмечены точки, определяющие минимаксную стратегию So второго игрока. [11]
 |
Отображение Шильникова ( а и пояснение наличия двух из бесконечного счетного множества подков ( б, в. [12] |
Следовательно, выбором достаточно малого е можно обеспечить такое взаимное расположение областей Z. D, как показано на рис. 6.10, так что становится очевидным присутствие подковы. Переходя к пределу е - 0, мы обнаруживаем присутствие бесконечного счетного множества подков. [13]
При этом на характеристики реактора данного размера влияют как взаимное расположение областей идеального смешения и вытеснения, Так и степень: егрегирования жидкости. [14]
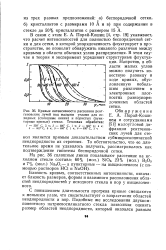 |
Кривые интенсивности рассеяния рентгеновских лучей под малыми углами для исходных ( сплошные линии и пористых ( пунктирные кривые стекол. Тепловая обработка. [15] |
Страницы: 1 2