Распределение - амплитуда - напряжение
Cтраница 2
Найденные таким образом функции распределения амплитуд напряжений используются далее для расчета на усталость. [16]
На рис. 14.1 показаны графики распределения амплитуд напряжения вдоль линии. Какому характеру нагрузок соответствует каждый из графиков. [17]
Для практики интересен случай, когда распределение амплитуд напряжений описывается логарифмически нормальным законом. [18]
В результате статистической обработки получают функции распределения амплитуд напряжений, характеризующие число повторений v / g амплитуд уровня оа / в одном блоке нагружения в случае ступенчатого задания этих функций. [19]
Повторяя многократно замеры и подсчеты функций распределения амплитуд напряжений в пределах данного сочетания регламентируемых факторов, получают различные функции распределения. [20]
Формулы (5.74) - (5.78) соответствуют функции распределения амплитуд напряжений, заданной в дискретной ступенчатой форме. [21]
 |
Корреляционная таблица совместного распределения амплитуд и средних напряжений цикла. [22] |
Повторяя многократно замеры и подсчеты функций распределения амплитуд напряжений в пределах данного сочетания регламентируемых факторов, получают различные функции распределения. [23]
В результате статистической обработки получают функции распределения амплитуд напряжений, характеризующие число повторений v / g амплитуд уровня оа / в одном блоке нагружения в случае ступенчатого задания этих функций. [24]
Это обеспечивает более точную оценку функций распределения амплитуд напряжений в области их максимальных значений. [25]
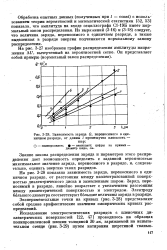 |
Зависимость заряда Q, переносимого в единичном разряде, от длины I промежутка плоскость - шар. [26] |
На рис. 3 - 27 изображен график распределения амплитуды напряжения At /, вычерченный на вероятностной сетке. [27]
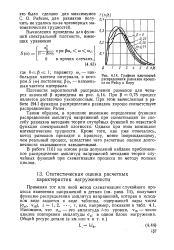 |
Графики плотностей распределения размг са по Раису и Виру. [28] |
Таким образом, в принципе возможно определение функции распределения амплитуд напряжений при схематизации по способу размахов методами теории случайных функций по известной функции спектральной плотности. Однако при этом возникают математические трудности. Кроме того, как уже отмечалось, метод размахов приводит к процессу, менее повреждающему, чем реальный процесс, вследствие чего расчетные оценки долговечности оказываются завышенными. [29]
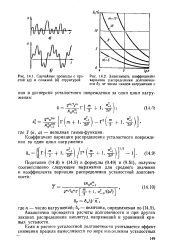 |
L Случайные процессы с про - [ IMAGE ] Зависимость коэффициента стой ( а и сложной ( б структурой вариации распределения долговечно05. [30] |
Страницы: 1 2 3 4