Распределение - интенсивность - поле
Cтраница 1
Распределение интенсивности поля в фокальной плоскости двухпорядкового фокусатора на рис, 5 606, полученное при циклическом сдвиге профиля (5.136) на тг / 65 подтверждает отсутствие спада интенсивности в центре креста. [1]
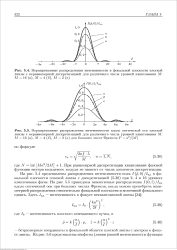 |
Нормированные распределения интенсивности в фокальной плоскости плоской с неравномерной для различного числа уровней М. [2] |
На рис. 5.4 представлены распределения интенсивности поля f ( p, 0) / 1ИД в фокальной плоскости плоской линзы с дискретизацией (5.38) при 2, 4 и 16 уровнях квантования фазы. [3]
 |
Спекл-интерферограмма н голографнческие ннтерферограммы, отражающие наклон объекта при регистрации спекл-поля в фурье-плоскости. [4] |
На рис. 91 представлен фотоснимок распределения интенсивности восстановленного поля в задней фокальной плоскости линзы при освещении двухэкспозиционной фурье-голограммы неразведенным лазерным пучком перпендикулярно поверхности голограммы. Поле в центре модулировано спекл-интерферограммой, тогда как боковые сопряженные изображения - топографической интерферограм-мой. Отчетливо видно, что количество интерференционных полос в автокорреляционном гало вдвое больше, чем на голографических изображениях. [5]
 |
Дифракционные картины от типичных апертур. Функции распределения IG ( 0, ф 12 пропорциональны. а - [ sin ( v / vf, v Ьаьтвсовф. б - [ sin ( va / va ] x. [6] |
Отсюда следует, что во всех плоскостях zq распределение интенсивности поля одинаково. Это свойство называют эффектом Талбота, или эффектом самовоспроизведения. Оно было впервые замечено Талбо-том в 1836 г. и имеет весьма важные приложения в фурье-спектроскопии и интерферометрии. [7]
Величина w есть, очевидно, ширина гауссова распределения интенсивности поля на расстоянии z от экрана ЕЕ. Согласно соотношению (43.6) квадрат ширины распределения на расстоянии z равен сумме квадрата исходной ширины ( wl) и квадрата ширины z / kw0, подсчитываемой по формуле для дифракции Фраунгофера ( ср. При z - оо ( практически при г J kwl - 2ядаоА) величина w стремится к значению z / kwa, характерному для фраунго-феровой дифракции. [8]
Величина w есть, очевидно, ширина гауссова распределения интенсивности поля на расстоянии z от экрана ЕЕ. Согласно соотношению (43.6) квадрат ширины распределения на расстоянии z равен сумме квадрата исходной ширины ( WQ) и квадрата ширины z / kwo, подсчитываемой по формуле для дифракции Фраунгофера ( ср. При z - оо ( практически при z kw 2тгШо / А) величина w стремится к значению z / kwo, характерному для фраунгоферовой дифракции. При малых z ( т.е. z C kw) ширина w переходит в WQ. [9]
В частности, там экспериментально показано, что итерационная процедура подбора оптимального диффузора для синтеза киноформа, предложенная в [140], для некоторых распределений интенсивности поля на объекте но сходится или, во всяком случае, сходится очень медленно. [10]
Для пояснения принципа голографии представим себе, что на плоскости, которая пересекает сферические волны точечного монохроматического источника света ( / - / на рис. 13.9, а), мы имеем возможность в одно мгновение зафиксировать распределение интенсивности поля. Такая мгновенная фотография представляет собой известную нам линзу Френеля. Если, убрав источник, осветить такую линзу с другой стороны параллельным пучком монохроматического света, то все лучи соберутся в одной точке, создавая изображение источника там, где он ранее находился. Два таких точечных источника в результате мгновенного фотографирования дадут на идеализированной фотопластинке две линзы Френеля, наложенные одна на другую. Их фокусные расстояния могут быть различны, если излучающие точки были удалены от плоскости на разные расстояния. [11]
Глория возникает, когда угол рассеяния отличается от угла падения 0j Ф О, тг / 2 на число, кратное тт. Распределение интенсивности поля в дальней зоне при рассеянии сферической частицей назад, соответствующее лучам глории, совпадает с распределением, которое дает кольцевой волновой фронт. Таким образом, в дальней зоне образуется центральное пятно с максимальной яркостью, окруженное кольцами с постепенно убывающей интенсивностью. [12]
 |
Регистрирующий слой голографического фотоматериала. [13] |
Дифракция света на голограмме обусловлена ее го-лограммной структурой, определяющейся пространственным распределением физических величин: показателя преломления и коэффициента поглощения света. Голограммная структура связана с го-лографической интерференционной структурой, зависящей от распределения интенсивности голографического поля в пространстве при получении голограммы. [14]
Результаты исследований особенностей взаимодействия полей ДФ позволяют распространить принцип компенсации дестабилизирующего воздействия поля ДФ характеристиками устойчивости элемента к воздействию соответствующего ДФ на этапе формирования стратегии размещения элементов, а этап ранжирования элементов для их установки в соответствии с определенной стратегией реализовать с учетом компенсирующего воздействия характеристик чувствительности параметров элементов к ДФ. Применение принципов суперпозиции и местного влияния [4], используемых при моделировании и расчетах полей ДФ, позволяет дифференцировать в составе комплексного воздействия собственную и наведенную составляющие интенсивностей полей соответствующих воздействий. Существенное влияние на стратегию размещения элементов оказывает наведенная составляющая ДФ, а собственная составляющая определяется характеристиками самого элемента и влияет на его выбор в процессе занятия позиций КП. Для большинства типовых конструкций наблюдается устойчивая тенденция к совпадению характера распределения наведенных составляющих полей основных ДФ. Функции распределения интенсивности поля этих составляющих ДФ от координат имеет куполообразную форму со смещением или вырождением центра купола при изменении граничных условий для описываемого поля ДФ. Таким образом, принятый для размещения элементов по критерию коммутационных свойств ресурсораспределительный подход на базе последовательного алгоритма обратного размещения можно обобщить на случай комплексного воздействия ДФ на объекты размещения. [15]
Страницы: 1 2