Распределение - интенсивность - рассеяние
Cтраница 1
Распределение интенсивности рассеяния качественно изменяется. [1]
Распределение интенсивности рассеяния рентгеновских лучей реальными кристаллами характеризуется типом и расположением дефектов решетки в пространстве. Однако решение точной задачи, когда таких дефектов много ( например, 104 и более), практически невозможно. Поэтому необходимо рассматривать усредненные величины, обосновывая соответствующие процедуры усреднения и используя характерные приемы сравнения с экспериментальными данными. [2]
Рассмотрим вклад в распределение интенсивности рассеяния рентгеновских лучей в направлении вдоль дифракционного вектора qt прямолинейных, хаотически распределенных в характерных для данной кристаллической решетки системах дислокационных мультиполей с равным числом дислокаций одного знака в мультиполе на примере дислокационных диполей. [3]
Эта теория устанавливает связь между наблюдаемой кривой распределения интенсивности рассеяния рентгеновских лучей в жидкости по углам и относительной частотой или вероятностью появления различных межатомных расстояний. [4]
Расчет распределения частиц латекса по размеру основывается на данных по распределению интенсивности рассеяния от латексных сфер, регистрируемого с помощью проточного ультрамикроскопа. [5]
В частности ими указывается на возможное влияние деформации решетки и ее движении на распределение интенсивности рассеяния, проявляющееся в увеличении диффузного рассеяния. Это может привести к завышенным результатам при определении аморфной части полимера. Поэтому точный анализ распределения интенсивности рассеяния рентгеновых лучей крайне затруднителен, и в большинстве случаев результаты определения кристалличности как уже приведенные выше, так и те, о которых речь еще впереди, получены без учета этого возможного влияния. [6]
В принципе распределение ориентации в аморфных областях полимеров может быть определено путем анализа распределения интенсивности рассеяния в аморфном гало. [7]
Первое слагаемое определяет интенсивность рассеяния атомами при отсутствии интерференции между ними; второе - распределение интенсивности рассеяния при наличии интерференции, обусловленной ближним порядком в расположении атомов. Третье слагаемое определяет интенсивность рассеяния в области очень малых углов. Числовое значение этого слагаемого зависит от размера и формы образца и не зависит от его внутренней структуры. При SL4 49 значения cp ( SL) малы по сравнению с единицей. Малоугловое рассеяние на образцах таких размеров совпадает с первичным пучком. Его интенсивность не может быть измерена с помощью обычных средств. Это рассеяние экспериментально обнаруживается в тех случаях, когда в исследуемом веществе имеются флуктуации, коллоидные частицы или макромолекулы размеромдо 103 А. [8]
Сравнивая формулы (8.148) и (8.149), видим, что при избытке дислокаций одного знака и дислокационных стенок полуширина распределения интенсивности рассеяния рентгеновских лучей пропорциональна величине qtb и отличается лишь коэффициентами, различие между которыми в общем случае экспериментально установить затруднительно. Однако форма кривой распределения для изгиба и дислокационных стенок резко отлична. [9]
По сравнению с дифракцией под большими углами рассеяние под малыми углами позволяет определить очень небольшое число параметров; так, распределение интенсивности непрерывного рассеяния для серии образцов целлюлозы позволило определить [11] радиусы инерции рассеивающих частиц ( 8 - 15 А), соответствующие цилиндрическим частицам диаметром 22 - 42 А. [10]
В начале 50 - х годов Уорреном и Авербахом [76-78] был предложен метод, в котором с помощью фурье-анализа физического уширения профиль линии на дебаеграмме ( или на дифрактограмме в методе 6 - 20-сканирования) разделяют вклад в распределение интенсивности рассеяния рентгеновских лучей от конечных размеров кристаллов ( или когерентно рассеивающих областей кристалла - блоков) и искажений ( или микроискажений кристаллической решетки) этих блоков. [11]
Исследуем дислокационные стенки, состоящие из дислокаций с одинаковым вектором Бюргерса. Распределение интенсивности рассеяния кристаллами с такими стенками оказывается качественно разным в зависимости от того, находятся ли дислокационные линии на строго одинаковом расстоянии друг от друга или распределены в стенке хаотически. [12]
В первом случае задаются определенной формой ( сфера, цилиндр и др.) и анизотропией отдельного рассеивающего элемента. Сопоставляя распределение интенсивности рассеяния по углам 0 и ц, полученное расчетным путем, с экспериментальной картиной С. Так, при исследовании пленок со сферолитной структурой сферо-литы моделируются однородными сферами, расположенными в изотропной среде. [13]
В первом случае задаются определенной формой ( сфера, цилиндр и др.) и анизотропией отдельного рассеивающего элемента. Сопоставляя распределение интенсивности рассеяния по углам 9 и ц, полученное расчетным путем, с экспериментальной картиной С. Так, при исследовании пленок со сферолитной структурой сферо-литы моделируются однородными сферами, расположенными в изотропной среде. [14]
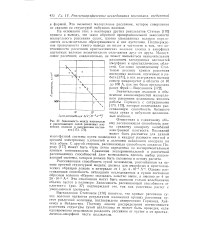 |
Зависимость между плотностью и рассеивающей силой различных вискозных волокон в высушенном состоянии. [15] |
Страницы: 1 2