Распределение - средняя интенсивность
Cтраница 1
Распределение средней интенсивности в плоскости фотокатода принято равномерным. [1]
С использованием этого соотношения масштаб рс находится из одновременных измерений распределения средней интенсивности в фокальных плоскостях двух идентичных приемных линз, одну из которых освещает исследуемый пучок, а вторую - плоская или сферическая волна. Измерения с источником неограниченной сферической или плоской волны необходимы для определения параметра а в (3.53) и значения структурной характеристики показателя преломления воздуха. [2]
Майкельсона от т0 до т - о, из графика распределения средней интенсивности в интерференционной картине ( интерферограмме) можно непосредственно определить временную корреляционную функцию светового поля. [3]
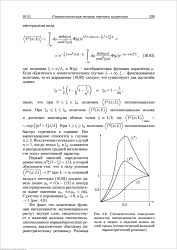 |
Схематическое поведение моментов интенсивности волнового поля в задаче о падении волны на слой среды ( стохастический волновой параметрический резонанс. [4] |
Исключение составляет случай п 1, когда точки и сливаются и распределение средней интенсивности носит монотонный характер. [5]
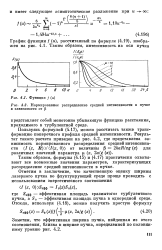 |
Функция / ( и.| Нормированное распределение средней интенсивности в пучке в зависимости от 6. [6] |
Таким образом, формулы (4.15) и (4.17) практически охватывают все возможные значения параметров, характеризувдщих распределение средней интенсивности в пучке. [7]
Функция взаимной когерентности То ( х, R, р) содержит также информацию о распределении средней интенсивности в поперечном сечении пучка и угловой структуре рассеянного излучения. [8]
Таким образом, изменяя временную задержку в схеме интерферометра Маикельсона от т 0 до т-оо, из графика распределения средней интенсивности в интерференционной картине ( интер-ферограмме) можно непосредственно определить временную корреляционную функцию светового поля. [9]
Следовательно, любой из методов анализа распределения интенсивности изображения для некогерентных систем, формирующих изображение, может быть применен для расчета распределения средней интенсивности спекл-структуры в изображении когерентно освещаемого шероховатого объекта. [10]
 |
Схема интерферометра Юнга. [11] |
Рассмотрим кратко оптические методы экспериментального определения пространственных и временных корреляционных функций, или, в терминах оптики, методы измерения пространственной и временной когерентности световых полей. Исторически понятие когерентности возникло в оптике в связи с интерпретацией результатов интерференционных опытов. Классические интерференционные опыты Юнга и Майкельсона оказываются прямыми методами измерения пространственных и временных корреляционных функций; распределение средней интенсивности в интерференционной картине непосредственно дает корреляционную функцию поля. Одновременно эти опыты можно рассматривать как схемы, поясняющие физический смысл пространственных и временных корреляционных функций. [12]
Следует, однако, отметить, что здесь ситуация оказывается более сложной. Дело в том, что, если модель стационарного случайного процесса хорошо описывает излучение многих источников света, случайные поля реальных световых пучков часто существенно отличаются от модели однородного случайного поля - пространственного аналога стационарного процесса. Угловые спектры реальных световых пучков определяются не только радиусом поперечной корреляции, но и геометрическими параметрами пучка, в частности распределением средней интенсивности в его поперечном сечении. Этот вопрос имеет большое значение для лазерной оптики; остановимся на нем подробнее. Итак, рассмотрим угловой спектр, соответствующий поперечной корреляционной функции неоднородного случайного поля. [13]
Страницы: 1