Распределение - капли
Cтраница 1
Распределение капель по размерам при тонком распыле можно исследовать в соответствии с законами вероятности, как это сделано в разд. [1]
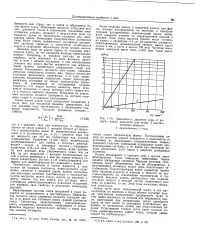 |
Зависимость давления пара от радиуса капли жидкости для низко - и высоко. [2] |
Распределение капель по величине широко изменяется в зависимости от источника их образования; конденсационная техника позволяет получать совершенно однородные капли ( монодисперсные системы), в то время как некоторые методы распыления дают капли с широким диапазоном размеров. [3]
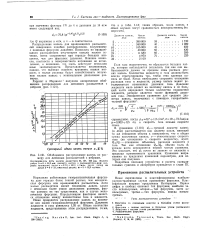 |
Обобщенное растределение капель по размеру для дисковых распылителей с ребрами. [4] |
Распределение капель для вращающихся распылителей совершенно подобно распределению, полученному с помощью форсунок давления. Поскольку во вращающихся распылителях отсутствуют каналы малого сечения, поток сохраняется при гораздо больших вяз-костях, чем для форсунок давления. Влияние вязкости, плотности и поверхностного натяжения не исследовано, и возможно, что здесь действуют несколько иные закономерности. Представляется несомненным, однако, что высокая скорость вращения, низкая вязкость и малые расходы будут способствовать получению мелких капель с минимальным диапазоном размеров. [5]
Распределение капель и порошков, выпускаемых с самолета, осуществляется в основном потоками воздуха, образующимися в процессе полета самолета. Такие потоки воздуха обусловлены мощными аэродинамическими силами, изменить которые для получения желательного распределения капель или порошка мо но только за счет изменения конструкции самолета. Так как эти изменения сделать нелегко, остается изучать существующие силы и конструкции и устанавливать рассеивающую аппаратуру так, чтобы использовать и дополнять воздушные потоки. Это означает управлять выпуском сельскохозяйственных препаратов с отдельных критических позиций с тем, чтобы полностью использовать аэродинамические силы. [6]
Распределение капель в факеле но числу и размерам весьма неравномерное. Следовательно, факел имеет неоднородную структуру. Скорость движения капель топлива и их количество возрастают по мере приближения к оси факела. [7]
Распределение капель ( пузырей) по размерам следует нормально-логарифмическому закону: вероятность логарифма доли капель текущего размера характеризуется нормальным распределением. Этот закон, присущий вообще большому числу случайных событий, установлен теоретически и подтвержден обширным экспериментом. При этом он оказался справедливым для широкого круга дисперсий, получаемых различными способами - как при диспергировании жидкостей и газов, так и при измельчении твердых материалов. [8]
Пусть распределение капель по размерам изменяется только за счет процесса коагуляции. [9]
Допустим распределение капель воды в нефти после заполнения отстойника равномерно. Следовательно, обводненность эмульсии в любом сечении ее одинакова и равна исходной обводненности В. [10]
Эволюция распределения капель по объемам n ( V, О описывается кинетическим уравнением (21.7), для решения которого необходимо знать выражения для скоростей изменения n ( V, О в правой части уравнения. [11]
Изучению распределения капель по размерам в лабораторных вибрационных колоннах посвящена также работа К. [12]
Изменение распределения капель по объемам n ( V, t, P) за счет коагуляции описывается уравнением (2.51), в правой части которого следует оставить только два первых слагаемых. [13]
 |
Зависимость скорости непрерывного роста капли от радиуса. [14] |
Функция распределения капель по размерам является одной из важнейших характеристик капельной конденсации. Попытки аналитического определения универсальной функции распределения наталкиваются на серьезные трудности. [15]
Страницы: 1 2 3 4