Распределение - концентрация - целевой компонент
Cтраница 1
Распределение концентрации целевого компонента при этом определяется только процессами молекулярно-диффузионного и конвективного переносов. [1]
Аналогичным образом формулируется задача для распределения концентрации целевого компонента в газовой фазе с р ( х, у), и обе эти задачи решаются совместно. [2]
Зависимости (2.59) и (2.60) описывают распределение концентрации целевого компонента во флегме и пленке по высоте исчерпывающей части зоны очистки. [3]
Если отсутствует движение жидкости, то распределение концентрации целевого компонента в ней является стационарным и не зависит от величины диффузионного вибрационного числа С. [4]
В результате реализации поинтервального метода рассчитывается распределение концентрации целевого компонента внутри частиц правильной геометрической формы. Существенная трудность анализа здесь состоит в том, что в каждый последующий интервал частицы входят со сложным начальным распределением компонента по радиусу, соответствующим конечному распределению на выходе из предыдущего интервала. [5]
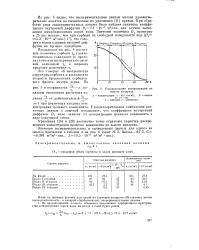 |
Распределение концентрации ио высоте аппарата. [6] |
Уравнения ( 26) и ( 28) достаточно точно отражают характер распределения концентрации целевого компонента по высоте аппарата. [7]
Классический метод разделения переменных Фурье состоит в том, что решение нестационарной задачи для распределения концентрации целевого компонента в неоднородном теле ищется в виде произведения двух функций, одна из которых зависит только от времени, а другая - от координаты. Использование такого проекта решения приводит к разделению уравнения в частных производных (1.45) на два дифференциальных уравнения в полных производных, каждое из которых, как правило, сравнительно легко решается, после чего общее решение оказывается возможным представить в виде бесконечного сходящегося ряда, коэффициенты которого определяются из начального условия задачи. [8]
Продвижение фронта фазового превращения в большинстве технологических процессов, как правило, оказывается весьма медленным, поэтому распределение концентрации целевого компонента поперек отработанной зоны ( /) в первом приближении полагается соответствующим стационарному распределению при мгновенном положении фронта. Для тела плоской формы такой квазистационарный профиль имеет линейный характер. [9]
Для того чтобы учесть неодинаковость концентраций целевого компонента в частицах твердой фазы при моделировании массообменных процессов вводят дополнительную переменную - функцию распределения концентрации целевого компонента в твердой фазе. [10]
В предыдущем разделе была рассмотрена задача о массооб-мене между газовым пузырьком и жидкостью в случае, если сопротивление массопереносу сосредоточено в дисперсной фазе. Если же массообменный процесс лимитируется внешнедиффузионной кинетикой, то необходимо решать задачу о распределении концентрации целевого компонента в потоке жидкости, окружающей газовый пузырек. [11]
 |
Формирование режима параллельного переноса фронта адсорбции при выпуклой изотерме и продольном. [12] |
При выпуклой изотерме эффекты расширения концентрационного фронта вследствие продольного перемешивания и сжатия фронта из-за выпуклости изотермы действуют в противоположных направлениях, что дает основание предполагать взаимную компенсацию этих двух эффектов на некоторой асимптотической стадии процесса, после чего должна происходить стабилизация концентрационного фронта и его последующее перемещение вдоль слоя параллельно самому себе. Может быть получено [2,25] асимптотическое решение для второй стадии режима параллельного переноса, которое дает прежнюю скорость перемещения сформировавшегося фронта (4.51) и распределение концентрации целевого компонента в потоке газа по длине слоя в форме квадратур, вычисление которых связано с конкретным видом уравнения изотермы адсорбции. [13]
Cs ( 0, z) / [ C ( z) ], что соответствует значению начальной концентрации в ионите, равновесной начальному распределению концентрации в жидкости. Граничное условие соответствует постоянному значению концентрации в потоке жидкости на входе в слой ( при z 0): С ( т, 0) Со. В рамках равновесной задачи распределение концентрации целевого компонента по радиусу зерен имеет естественный равномерный характер. [14]
Решение дифференциального уравнения (1.15) должно определить нестационарное распределение концентрации целевого компонента по координатам. В такой общей постановке задача о распределении концентрации компонента аналитическими методами не решается. Более того, даже при известных зависимостях wx, wv и wz от координат и от времени уравнение (1.15) не может быть проинтегрировано в общем виде. Теоретическое рассмотрение задачи о распределении концентрации целевого компонента в движущемся потоке вязкой среды возможно только в предельно упрощенных случаях. [15]
Страницы: 1 2