Распределение - концентрация - частица
Cтраница 3
Однако для глубокой потенциальной ямы в точном решении временного уравнения (2.9) необходимости нет, так как достаточно решить стационарную задачу, подобную той, которую мы выполнили в § 4, когда рассматривали время достижения блуждающей точкой границ определенной области. Вспомним описанный там метод решения задачи. Сначала находится распределение концентраций частиц, возникающее, когда в системе создается стационарный поток частиц, затем - общее число частиц в интересующей нас области. [31]
Первый раздел главы 3 посвящен обзору исследований в области физико-математического моделирования процесса смешения твердых частиц с высокоскоростными потоками газа, возникающего при действии ударных волн, волн сжатия и разрежения на неустойчивые пылевые отложения, расположенные на границах каналов, на пластинах, в кавернах, и на свободные облака частиц. Описываются, в частности, эксперименты в ударных трубах с частицами, лежащими первоначально в кавернах и на поверхностях. Экспериментальные данные, которые представлены в виде распределений концентрации частиц в различных точках пространства по высоте над неустойчивым слоем, распределений давления на нижней стенке ударной трубы, используются исследователями для верификации разработанных математических моделей как в режимах одиночных частиц и взаимодействующих континуумов, так и турбулентной диффузии. [32]
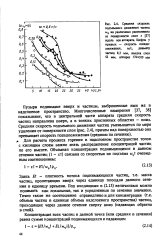
Пузыри поднимают вверх и частицы, выброшенные ими же в надслоевое пространство. Многочисленные измерения [37, 38] показывают, что в центральной части аппарата средняя скорость частиц направлена вверх, а в тонких пристенных областях - вниз. Средняя скорость подъемного движения частиц уменьшается по мере удаления от поверхности слоя ( рис. 2.4), причем над поверхностью она превышает скорость псевдоожижения ( среднюю по сечению), г Для расчета процесса горения в надслоевом пространстве топок с кипящим слоем важно знать распределение концентраций частиц по его высоте. [34]
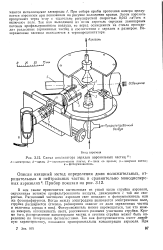 |
Схема анализатора зарядов аэрозольных частиц п. [35] |
В нем также применяется вытекающая из узкой щели струйка аэрозоля, окруженная потоком профильтрованного воздуха, движущимся с той же скоростью. Рассеянный частицами аэрозоля свет попадает в фотоумножитель или же фотографируется. Фотоумножитель может перемещаться, так что можно измерить интенсивность света, рассеянного разными участками струйки. Кроме того, распределение концентрации частиц в сечении струйки может быть определено по почернению фотопластинки. Так как фотоумножитель имеет линейную характеристику, показания пропорциональны концентрации аэрозоля. [36]
Как видно из таблицы, пульсационные скорости частиц, найденные киносъемкой и по турбулиметру, в одних случаях близки, а в других сильно различаются. Кроме того, пульсационные скорости, подсчитанные по турбулиметру, с ростам скорости фильтрации сначала возрастают, а затем начинают резко убывать, тогда как кинематографически измеренные скорости не обнаруживают подобной тенденции, по крайней мере в данном диапазоне скоростей фильтрации. Расхождения могут объясняться или действительным различием пульсаций на периферии и в средине слоя, или погрешностями опытов с тур-булиметром. В качестве теоретического обоснования выдвигается соображение, что при очень больших числах псевдоожижения сильно возрастает по-розность слоя, а гидродинамические силы притяжения между частицами убывают примерно обратно пропорционально четвертой степени расстояния между части - цами. Однако в разреженном псевдоожиженном слое могут быть сильны иные гидродинамические эффекты, вызывающие интенсивное движение частиц, как, например, известный эффект Магнуса. Для выяснения надежности результатов, полученных с помощью турбулиметра, необходимы сведения о распределении концентраций частиц по слою в условиях проведенных опытов. [37]
Этому противодействуют факторы, способствующие концентрации частиц и процессов в малых объемах. Если бы процессы дугового цикла в пределах данной ячейки находились постоянно в равновесии, то в результате одновременного действия рассеивающих и концентрирующих процессов должно было бы установиться некоторое равновесное распределение концентрации частиц и интенсивности процессов по сечению ячейки. Так как в установлении этого распределения играет большую роль фактор рассеяния энергии в окружающее пространство, его можно было бы описать монотонно убывающей функцией от центра ячейки к периферии, подобной нормальной функции распределения или кривой ошибок Гаусса. Но такого рода равновесное распределение симметричного типа является идеализацией, не отвечающей ни в какой мере действительности. Вследствие нарушений равновесия между отдельными процессами дугового цикла в пределах каждой ячейки, а также под влиянием случайных флуктуации в распределении частиц и различного рода внешних воздействий на ячейку симметрия и равновесие всех четырех областей должны непрерывно нарушаться. Ввиду существующей связи между областями эти изменения способны привести к смещению на новый участок всей ячейки. Особенно чувствительным к любым изменениям распределения концентрации частиц должен быть процесс автоэлектронной эмиссии в силу его безынерционности и резкой зависимости от напряженности поля. Результатом этого должны явиться чрезвычайно высокая изменчивость и подвижность области эмиссии Se. Напротив, область испарения катода ST, скорость перемещения которой лимитируется инерционным процессом нагревания металла, должна обладать наиболее низкой подвижностью, ограничивая скорость перемещения всей ячейки в целом. Отказываясь от невыполнимой задачи проследить все не поддающиеся контролю изменения, которые претерпевает с течением времени область эмиссии, тем не менее мы можем учесть их конечный результат в смысле воздействия на область испарения. [38]
При напряженности порядка 1 000 э, которой может обладать собственное поле дуги в районе пятна, отклонение траекторий электронов от силовых линий в малой области поля составляет всего лишь около 0 03 мм. Вопрос осложняется, однако, тем, что правило соответствия в строгом смысле применимо лишь к ограниченной области поля, размеры которой зависят от характера и степени его неоднородности, а также от плотности среды и напряженности электрического поля. Эти ограничения связаны с тем, - что все названные факторы служат источником дополнительного отклонения электронных траекторий от магнитных силовых линий, увеличивающегося по мере поступательного движения электронов. Такого рода отклонение прежде всего вызывает сама неоднородность поля, связанная с - кривизной силовых линий, причем отклонение должно быть, направлено по нормали к плоскости, в которой лежит данный участок кривой. Существенной неоднородностью указанного типа в рассматриваемых ниже условиях опыта обладает лишь собственное магнитное поле дуги в районе катодного пятна. Однако силовые линии этого поля представляют собой преимущественно плоские кривые, расположенные в плоскости нормального сечения разряда. Поэтому отклонение электронов, обусловленное кривизной линий, должно быть направлено всегда вдоль оси разряда и, следовательно, не может отразиться заметным образом на распределении концентрации частиц вокруг границ катодного пятна. [39]
Канал ударной трубы был выполнен из алюминия, его длина 7 м, размер сечения 40 х 80 мм. Частицы пыли достигают высоты, на которой расположен зондирующий лазерный луч, за конечное время. Приведены зависимости этого времени от расстояния, на котором расположена точка от поверхности, для чисел Маха 1.92 и 2.48, а также зависимости высоты подъема облака от времени и распределения концентрации частиц в облаке в некоторой фиксированной точке, расположенной вблизи от конца кюветы. Дана аппроксимационная зависимость, выражающая экспоненциальный закон распределения концентрации по высоте с показателем в экспоненте и предэкспоненте, определяемыми временем процесса. [40]
Страницы: 1 2 3