Распределение - коэффициент - теплоотдача
Cтраница 1
Распределение коэффициента теплоотдачи по высоте трубы оказывается качественно одинаковым как при электрическом, так и при конденсационном обогреве. Однако при электрообогреве вследствие большой тепловой нагрузки в зоне подогрева жидкость быстрее нагревается и закипает. [1]
Распределение коэффициентов теплоотдачи по поверхности цилиндра или сферы при Рг - 0 и Рг - оо также различно. [2]
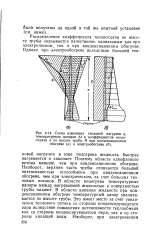 |
Схема изменения тепловой нагрузки q, температурных напоров At и коэффициентов теплоотдачи а по высоте трубы Я при конденсационном обогреве ( а и электрообогреве ( б. [3] |
Распределение коэффициента теплоотдачи по высоте трубы оказывается качественно одинаковым как при электрическом, так и при конденсационном обогреве. [4]
Степень неравномерности в распределении коэффициентов теплоотдачи для разных участков исследуемой на модели поверхности нагрева ( соответственно рассмотренным выше случаям усреднения локальных коэффициентов теплоотдачи), может быть подсчитана применительно к одной трубке, отдельным сечениям, определенным участкам или всей поверхности нагрева. [5]
Конечным результатом исследования являются распределения коэффициентов теплоотдачи и числа Стантона, которые приведены на фиг. [6]
На рис. 3.3.17 показано распределение коэффициентов теплоотдачи по поверхности шины, знание которых необходимо при решении прямой или обратной задачи о температурном поле в нагруженной шине с учетом теплообразования в ней. [7]
При / Vcl меняется как характер распределения коэффициента теплоотдачи по окружности трубы, так и его зависимость от скорости набегающего потока. [8]
При Рг; Г меняется как характер распределения коэффициента теплоотдачи по окружности трубы, так и его зависимость от скорости набегающего потока. [9]
Таким образом природа поправочного множителя со всецело определяется неравномерностью распределения коэффициента теплоотдачи на поверхности ребра. [10]
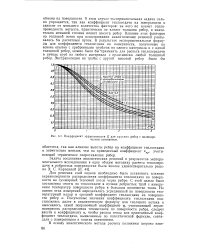 |
Коэффициент эффективности Е для круглых ребер с цилиндрическим основанием. [11] |
Для решения этой задачи необходимо было установить влияние неравномерности распределения коэффициента теплоотдачи по поверхности на суммарный тепловой поток через ребро. С этой целью были поставлены опыты по теплоотдаче в пучках ребристых труб с измерением температур поверхности ребра в большом количестве точек. На основе этих измерений определялись усредненный по поверхности температурный напор и средний коэффициент теплоотдачи на поверхности ребер а. Полученные значения коэффициента теплоотдачи подставлялись далее в аналитическую формулу для теплового потока и выяснялось, какой поправочный коэффициент г), учитывающий неравномерность распределения теплоотдачи по поверхности ребра, следует ввести к коэффициенту а, чтобы расход тепла или приведенный коэффициент теплоотдачи, вычисленные по аналитической формуле, совпадали с измеренными в опытах значениями. [12]
Как и в слое мелких частиц, при у 30 ввиду хорошего перемешивания частиц и газа распределение коэффициентов теплоотдачи по высоте пластины практически равномерно. [13]
Для того чтобы дополнить данные по локальным коэффициентам теплоотдачи, полученные Г. А. Михайловым и Л. С. Эйгенсоном, исследовалось распределение коэффициентов теплоотдачи преимущественно по поверхности труб тесных пучков. [14]
Эту последнюю можно выразить как произведение средней температуры ребра Tw на коэффициент со, который учитывает неравномерность распределения коэффициента теплоотдачи по поверхности ребра. [15]
Страницы: 1 2