Распределение - напор
Cтраница 1
Распределение напора по высоте между верстиями дано на эпюре фиг. [1]
Хотя распределение напора вдоль радиуса в радиальных и осевых насосах сходно, имеется существенная разница в обоих случаях между конечными результатами. [2]
Эпюра распределения напоров по глубине на стенке завесы, обращенной к нижнему бьефу, показана на чертеже. [3]
 |
Схема к формулам ( П. 80 и. [4] |
Мы получили распределение напора в пласте, обусловленное течением, имеющим и гравитационную, и элизионную составляющие. Совершенно ясно, что это не точное распределение напора, а некоторое приближенное для случая, когда отсутствуют перетоки из одного водоносного пласта в другой. [5]
Расчетная гистограмма распределения напоров одного из серийных насосов приведена на рис. 2.19 о. [6]
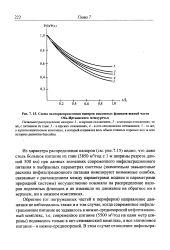 |
Схема палеораспределения напоров подземных флюидов южной части. [7] |
Из характера распределения напоров ( см. рис. 7.15) видно, что даже столь большое питание из глин ( 3850 м3 / год с 1 м ширины разреза длиной 500 км) при данных значениях современного инфильтрационного питания и выбранных параметрах системы ( значительно завышенные расходы инфильтрационного питания нивелируют возможные ошибки, связанные с расхождением между параметрами модели и параметрами природной системы) несущественно повлияло на распределение напоров подземных флюидов и не изменило их движение на обратное ни в верхнем, ни в нижнем комплексах. [8]
Выполнен гармоничный анализ распределения напора ( давления) по внешнему периметру рабочего колеса для учета конечного количества лопастей насоса Кл. Поскольку полезная работа, которая выполняется рабочим колесом РЦН, есть результатом его силового взаимодействия с потоком благодаря разности давлений напорной и всасывательной сторон лопастей, то распределение напора Нт ( 12) по внешнему периметру колеса / 2 имеет вид периодической нелинейной функции угла 9 с периодом Т 2тг / Кл с разрывом непрерывности в местах положения лопастей, которое можно путем замены 9i - 9КЛ разложить в тригонометрический ряд Фурье. [9]
Выполнен гармонический анализ распределения напора ( давления) по внешнему периметру рабочего колеса для учета конечного числа лопастей насоса. Создана математическая модель ЦН во вращающейся системе координат, жестко связанной с колесом насоса. Синтезированы развернутая и эквивалентная комплексные схемы замещения гидромашины, построены векторная и круговая диаграммы равновесия расходов и давленный ЦН, позволяющие осуществить аналитический учет влияния изменения частоты вращения колеса насоса и вязкости рабочей жидкости на характеристики ЦН. Предложена методика и программа итерационного расчета на ЭВМ параметров комплексной схемы замещения гидромашины и создан на ее основе банк этих параметров для серии ЦН магистральных нефтепроводов. Использован метод электрогидравлической аналогии для определения и контроля параметров схемы замещения ЦН. Установлен изоморфизм математических выражений, описывающих реальный ЦН и синхронную электрическую машину переменного тока. [10]
Для получения картины распределения напоров ( давлений) подземных флюидов, а следовательно, и оценки направлений и скоростей их движения необходимо решать уравнение 4.1 с заданными граничными и начальными условиями. Таким образом, задача сводится к правильному обоснованию граничных условий и нахождению достоверных значений коэффициентов. При этом, как и при решении других вопросов геологии, может быть широко использован принцип актуализма и геологические методы исследования, в том числе и метод моделирования. [11]
Исходя из закономерностей распределения напоров в пластовой системе глубина залегания этого элемента будет соответствовать подошве первого гидрогеологического этажа, а не нижней границе зоны интенсивного водообмена, как считает Н. А. Журавель ( см. гл. Однако такое изменение будет свидетельствовать о том, что на определенном уровне разреза ( в зоне разгрузки, нейтральной полосе или области питания) распределение напоров межпластовых вод с увеличением глубины залегания уже не соответствует условиям, характерным для первого гидрогеологического этажа. [12]
Дифференциальные уравнения фильтрации описывают распределение напора ( давления) в фильтрационном потоке. Для их вывода в уравнении неразрывности компоненты скоростей фильтрационного потока выражаются из закона фильтрации, а деформации пласта ( воды и породы) связываются с давлениями через уравнения состояния. [13]
Полученная формула позволяет определить распределение напора Я вдоль основания флютбета. [14]
Коэффициент А3 зависит от распределения напора, восстанавливаемого эжектором ( Арс - f - Арк) между цилиндрической камерой смешения и диффузором. [15]
Страницы: 1 2 3 4 5