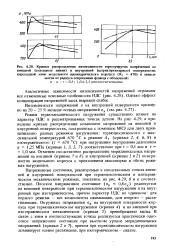
Распределение - меридиональное напряжение
Cтраница 1
Распределение меридиональных напряжений показано штриховыми, а окружных напряжений и перемещений - сплошными линиями. [1]
Влияние изгиба на распределение меридиональных напряжений в очаге деформации учитывается при определении граничных условий на стыке смежных участков разной кривизны. При этом считается, что на стыке таких участков, в точке резкого изменения кривизны в меридиональном сечении, напряжение стр скачкообразно увеличивается по модулю на Аар, определяемое по приведенным ранее формулам. [2]
На рис. 3 и 4 показаны распределения меридиональных напряжений вдоль образующей аппарата для его внутренней и наружной поверхностей для случаев смещения кромок с 0; s / 4; - s / 4, где s - толщина стенки днища. [3]
На рис. 8 и 9 показаны распределения меридиональных напряжений вдоль образующей аппарата для его внутренней и наружной поверхностей для случаев смещения кромок с 0; s / 4; - s / 4, где s - толщина стенки днища. Толщины днищ и цилиндрических обечаек были приняты одинаковыми. [4]
На рис. 52, г показано распределение меридиональных напряжений в зоне краевого эффекта ( соединения корпуса с крышкой) по толщине и по образующей. В этом случае максимальные напряжения могут в несколько раз превышать напряжения, рассчитанные по безмоментной теории. Дальнейшее увеличение давления при-водит к распространению пластических деформаций по длине образующей цилиндра. В предельном состоянии, как показывают испытания, цилиндр принимает бочкообразную форму, когда зона пластических деформаций охватывает весь цилиндр. [5]
Основываясь на сказанном, допустимо принять, что при отыскании распределения меридиональных напряжений в условиях осевой симметрии деформирования влиянием изменения кривизны в широтных сечениях можно пренебречь. [6]
Если же учесть, что на величине меридиональных напряжений действие широтных моментов скажется через проекцию широтных напряжений на касательную к образующей заготовки, можно полагать, что незначительное изменение широтных напряжений, вызванное действием широтных моментов, скажется на величине и распределении меридиональных напряжений в весьма малой степени. [7]
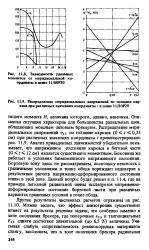 |
Зависимость удельных моментов от меридиональной координаты в шине 11 / 80Р20.| Распределение меридиональных напряжений по толщине каркаса при различных значениях координаты t в шине 11 / 80Р20. [8] |
Я, величина которого, однако, невелика. Описанная ситуация характерна для большинства радиальных шин, обладающих мощным силовым брекером. Распределение меридиональных напряжений a, , по толщине каркаса ( 0 z 0 33 см) при различных значениях координаты t проиллюстрировано рис. 11.9. Анализ приведенных зависимостей убедительно показывает, что напряженное состояние каркаса в беговой части ( О г 12 см) является существенно моментиым. Боковина же работает в условиях безмоментного напряженного состояния. Бортовую зону здесь не рассматриваем, поскольку неясность с граничными условиями в точке обода порождает недоверие к результатам расчета напряженно-деформированного состояния шины в этой зоне. [9]
Режим термо механического нагружения существенно влияет на характер НДС в рассматриваемых точках детали. На рис. 4.29, а приведены кривые распределения компонент напряжений на внешней и внутренней поверхностях, построенные с помощью МКЭ для двух принципиально разных режимов нагружения: термоциклического с максимальной температурой 670 С в режиме А1 ( кривые 2, 4, 6, 8) и изотермического ( t 670 С) при нагружении внутренним давлением q 1 25 МПа ( кривые 1, 3, 5, 7) соответственно при г 0 5 мм и г 1 0 мм. Отметим сходственное распределение меридиональных напряжений на внешней ( кривые 7 и 8) и внутренней ( кривые 1 и 2) поверхностях модельного корпуса с проявлением максимума в обоих режимах нагружения. [11]
Режим термомеханического нагружения существенно влияет на характер НДС в рассматриваемых точках детали. На рис. 4.29, а приведены кривые распределения компонент напряжений на внешней и внутренней поверхностях, построенные с помощью МКЭ для двух принципиально разных режимов нагружения: термоциклического с максимальной температурой 670 С в режиме At ( кривые 2, 4, 6, 8) и изотермического ( f 670 С) при нагружении внутренним давлением q 1 25 МПа ( кривые 1, 3, 5, 7) соответственно при г 0 5 мм и г 1 0 мм. Отметим сходственное распределение меридиональных напряжений на внешней ( кривые 7 и 8) и внутренней ( кривые 1 и 2) поверхностях модельного корпуса с проявлением максимума в обоих режимах нагружения. [13]
Эпюры меридиональных термоупругих напряжений в тонкостенном оболочечном цилиндрическом корпусе для характерных тепловых режимов А1 - АЗ, приведенные на рис. 4.13, подобны. Это означает, что для соответствующих кривых распределения напряжений существует коэффициент подобия, с помощью которого можно получить кривую, совпадающую с базовой. Приняв, например, в качестве базовой кривую распределения меридиональных напряжений в режиме АЗ ( кривая / на рис. 4.15, а), приведенные кривые напряжений для других тепловых состояний получим с помощью очевидных преобразований: ( as) Ai Кг ( а5) Аз ( кривая 2) и ( as) Aj К2 ( а5) Аз ( кривая 3), где Jfj, К2 - коэффициенты подобия. [14]
Эпюры меридиональных термоупругих напряжений в тонкостенном оболочечном цилиндрическом корпусе для характерных тепловых режимов AI - А3, приведенные на рис. 4.13, подобны. Это означает, что для соответствующих кривых распределения напряжений существует коэффициент подобия, с помощью которого можно получить кривую, совпадающую с базовой. Приняв, например, в качестве базовой кривую распределения меридиональных напряжений в режиме АЗ ( кривая 1 на рис. 4.15, а), приведенные кривые напряжений для других тепловых состояний получим с помощью очевидных преобразований: ( os) Al Ki ( s A3 ( кривая 2) и ( о) Лз К2 ( о5) Аз ( кривая 3), где Кг, К2 - коэффициенты подобия. [15]
Страницы: 1 2