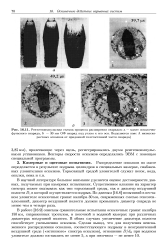
Распределение - осколки
Cтраница 2
Очень интересные результаты были получены при сравнении формы кривой распределения осколков по массам для разных энергий возбуждения делящегося ядра. [16]
При повышении энергии возбуждения деление постепенно симметрируется, и кривая распределения осколков по массам становится одногорбой. [17]
Изложенная теория предсказывает наличие трех различных областей х, связанных с распределением осколков по размерам: область постоянной дифференциальной вероятности р для малых х, в которой преобладающую роль играют краевые дефекты; по мере увеличения х за этой областью следуют две другие, соответствующие влияниям поверхностных и объемных дефектов. Последняя область ранее экспериментально не была обнаружена. Между тем экспериментально доказано, что рассматриваемое явление существует. Экспериментальная кривая зависимости дифференциального параметра р от х имеет два пика, соответствующие влияниям поверхностных и объемных дефектов в образце. [18]
Так как при р-распаде меняется заряд осколков, а их массовое число остается постоянным, то распределение осколков деления характеризуют не по зарядам, а по массам. Кривая рис. 12 имеет два горба ( максимумы), которые соответствуют массовым числам изотопов, получаемых с наибольшим выходом. [19]
Это соотношение можно выразить через любое другое среднее значение степени полимеризации СП при условии, что характер распределения осколков по размерам не меняется на протяжении всего процесса деструкции. [20]
Конкретные значения чисел а, Ь, с и d в каждом акте деления могут быть различными, так как зависимость распределения осколков от их массовых и зарядовых чисел носит вероятностный характер. [21]
Хотя деление ядер, например урана, в основном объясняется деформациями капли ядерной жидкости, сдерживаемой ядерными и разрываемой электрическими силами, однако тонкая структура кривой распределения осколков отчетливо показывает влияние оболочек, как было выяснено после более тщательных опытов. [22]
Распределение осколков по массе определяется в результате подрыва цилиндров в специальных камерах, снабженных уловителями осколков. [24]
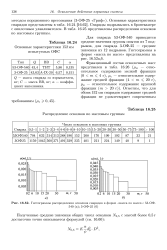 |
Гистограммы распределения осколков снарядов в форме масса по массе. 53 - ОФ. [25] |
В табл. 16.25 представлены распределения осколков по массовым группам. [26]
Сложная картина распределения осколков по массам наблюдается при делении относительно легких ядер. При делении 22eRa протонами с энергией 11 МэВ наблюдается трехгорбое распределение осколков по массам - один горб соответствует симметричному, два других - асимметричному делению. С ростом энергии возбуждения выход симметричного деления растет. Для еще более легких делящихся ядер ( Bi - f - d), у к-рых деление становится заметным лишь при энергии возбуждения св. [27]
Наиб, характерная его особенность при небольшой энергии возбуждения - асимметрия распределения осколков по массе. [28]
Чтобы учесть в теории такое вырождение дефектов, необходимо предпринять существенный предварительный шаг - построение теории на основе биноминального распределения, которое не ограничивается бесконечным числом событий. Недавно Годин и Мэлой 15, принимая биноминальное распределение, вывели функцию распределения осколков по размерам при одноразовом разрушении. В оригинальной форме их модель не может учесть влияния поверхностных и объемных дефектов, на фактическое существование которых указывают эксперименты. Следует - упомянуть, что результаты Година и Мэлоя отличаются от выводов Мэннинга 34, который ранее рассматривал ту же самую математическую задачу другим методом. [29]
К другому общему типу функций распределения относится эмпирическое соотношение Розина и Рэмлера16 - 38, в котором размеры частицы входят в аргумент показательной функции. Как будет показано, этот тип распределений применим, когда условия эксперимента приблизительно соответствуют однократному разрушению. Однако ни одна из многочисленных попыток статистического или физического обоснования подходящей функции распределения осколков по размерам при однократном разрушении тела не является достаточно строгой или достаточно плодотворной. [30]
Страницы: 1 2 3