Распределение - вейбул
Cтраница 1
 |
Распределение экстремального значения наибольшего ( / и наименьшего ( 2 элемента для. [1] |
Распределение Вейбула описывает распределение ожидаемого времени отказа в работе большой разновидности сложных механизмов. [2]
Дубинин, применив распределение Вейбула, наш. [3]
В период приработки внезапные отказы описываются распределением Вейбула с параметром т1 или гамма-распределением. В период повышенного износа или старения объекта отказы описываются усеченным нормальным распределением или распределением Релея. [4]
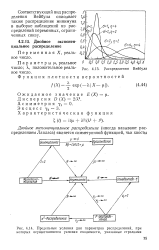 |
Предельные условия для параметров распределений, при которых осуществляются условия сходимости, указанные стрелками. [5] |
К, положительное реаль - Рис 4.13. Распределения Вейбула ное число. [6]
В работе [114], исходя из функции распределения Вейбула, проведено определение вероятности безотказной работы стальных труб в агрессивных средах. Для этого проведено прогнозирование коррозионной стойкости материала труб. Из вида функции распределения с учетом коррозионного прогноза определен оптимальный межремонтный период для технологической системы. [7]
Приведено новое характеристическое уравнение, основанное на более общей функции распределения Вейбула. [8]
Вместе с разновидностью 1 - е-х они появляются ( несколько таинственно) под именем распределении Вейбула. [9]
В работе В. А. Астахова, М. М. Дубинина, Л. П. Машаровой и П. Г. Романкова [154] показано, что величины Е и п являются параметрами распределения Вейбула, связанными между собой, и их величина определяется потерей некоторого количества степеней свободы у молекулы в результате ее адсорбции на поверхности твердого тела. При адсорбции на непористых сорбентах, как полагают авторы этой работы, теряется одна поступательная степень свободы, что соответствует в уравнении ( III. [10]
 |
Влияние объема на прочность по статистическим моделям. [11] |
Среди этих трещин выделяется опасная. Статистическая теория в традиционном варианте основана на распределении Вейбула и исходит из того, что вероятность появления опасной трещины в малом объеме меньше, чем в большом, отсюда и повышенная вероятность разрушения большого образца. [12]
На рис. 1, 2 и 3 приведены функции распределения значений показателей физико-механических свойств пыли. Функция распределения / ( рп) значения насыпной плотности пыли ( рис. 1) изображена на вероятностной сетке закона нормального распределения. Функции распределения F ( w) и F ( T значений относительной влажности и температуры пыли ( рис. 2) даны на вероятностной сетке закона распределения Вейбула. [13]
Страницы: 1