Распределение - непрерывная случайная величина
Cтраница 4
При решении задач, которые выдвигает практика, приходится сталкиваться с различными распределениями непрерывных случайных величин. Плотности распределений непрерывных случайных величин называют также законами распределений. Часто встречаются, например, законы равномерного, нормального и показательного распределений. В настоящем параграфе рассматривается закон равномерного распределения вероятностей. Нормальному и показательному законам посвящены следующие две главы. [46]
 |
Многоугольник вероятности. [47] |
Помимо описательного представления вида распределения пользуются и специальными аналитическими средствами. Например, закон распределения непрерывной случайной величины X количественно выражают в двух формах: с помощью так называемой функции распределения либо плотности распределения случайной величины. [48]
Эта формула определяет f ( x) во всех точках ее непрерывности, т.е. при всех ж, кроме, может быть, некоторого множества точек нулевой суммарной меры. Следовательно, она полностью определяет распределение непрерывной случайной величины. [49]
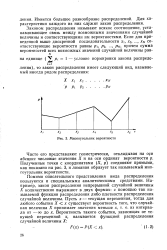
График этой функции - монотонная кривая, возрастающая от нуля до единицы. На рис. 13 изображены примеры функций плотности распределения непрерывной случайной величины. На рис. 13, а изображена функция плотности для ограниченной случайной величины, на рис. 13 6 - для неограниченной случайной величины. [50]
Проделана определенная работа и по теории вероятностей. Исхаков предложил и исследовал оригинальную процедуру сравнения законов распределения непрерывных случайных величин. [51]
Страницы: 1 2 3 4