Распределение - данная случайная величина
Cтраница 1
Распределение данной случайной величины X найдено в примере 1 предыдущего пункта. [1]
Составим таблицу распределения данной случайной величины. [2]
Характер зависимости у от х называется законом распределения данной случайной величины. Характер распределения случайной величины может быть выражен также при помощи основных численных характеристик - щентра группирования отклонений и меры рассеяния отклонений от этого центра. [3]
Для доверительной оценки полученного среднего значения необходимо установить вид функции распределения данной случайной величины. По виду вариационного ряда можно предположить, что вероятность отказа трубы подчиняется экспоненциальному закону распределения. [4]
Часто из тех или иных соображений можно предположить, что функция распределения данной случайной величины ( генеральной совокупности) имеет вид, принадлежащий некоторому типу распределений; например, что генеральная совокупность имеет нормальное распределение, показательное распределение или какой-либо другой вид распределения. Таким образом, выдвигается некоторая гипотеза. Для подтверждения или отклонения данной гипотезы рассматривают некоторую выборку, которая извлечена из данной генеральной совокупности. Определяют по вариантам данной выборки значения параметров, входящих в формулу теоретической функции распределения. Заменяя найденные значения параметров в формулах функции распределения, получим конкретную функцию, которая является аппроксимацией выборочных распределений теоретическими распределениями. Таким образом, распределения конкретных выборок аппроксимируются теоретическими. Сопоставляя полученные результаты с данными практики, принимаем или отвергаем выдвинутую гипотезу о виде функции распределения. [5]
Соответствие между всеми возможными значениями дискретной случайной величины и их вероятностями называется законом распределения данной случайной величины. [6]
Такие кривые называются теоретическими кривыми распределения, а характер зависимости Y от х - законом распределения данной случайной величины. [7]
Соответствие между всеми возможными значениями дискретной случайной величины и их вероятностями на-в: гвается законом распределения данной случайной величины. [8]
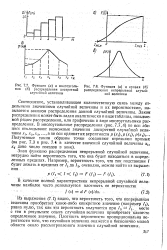 |
Функция ( а и многоуголь - [ IMAGE ] Функция ( а и кривая ( б ник ( б распределения дискретной распределения непрерывной случай-случайной величины ной величины. [9] |
Соотношение, устанавливающее количественную связь между отдельными значениями случайной величины и их вероятностями, называется законом распределения данной случайной величины. Закон распределения может быть задан аналитически в виде таблицы, называемой рядом распределения, или графически в виде многоугольника распределения. [10]
В табл. 39 указаны значения вероятности отказа в обслуживании, определенные методом моделирования, при распределении времени обслуживания и ожидания по законам: показательному, Релея, усеченному нормальному, равновероятному. Из табл. 39 видно, что закон распределения данных случайных величин практически не влияет на точность полученных оценок. Поэтому допущения о показательном законе, сделанные во всех ранее рассмотренных случаях, не приводят к значимым для практических целей погрешностям. [11]
Страницы: 1