Распределение - указанная величина
Cтраница 1
Предположение относительно нормальности распределения указанных величин не входит в проверяемую гипотезу. [1]
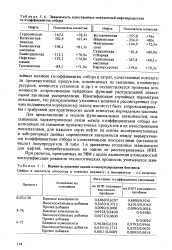 |
Зависимость качественных показателей нефтепродуктов от коэффициентов отбора. [2] |
Идентификация случайных параметров показывает, что распределения указанных величин в рассмотренных случаях подчиняются нормальному закону или могут быть аппроксимирова - ны с требуемой для практических целей точностью нормальным законам. [3]
Во многих случаях оказывается, что распределение указанных величин хорошо аппроксимируется с помощью биномиального, пуассоновско-го, отрицательного биномиального или экспоненциального законов. Поэтому в практической работе эти законы используются наиболее часто. [4]
Этот результат противоречит общепринятому мнению, согласно которому распределение указанных величин следует логарифмически нормальному закону. Различие чрезвычайно значительно, так как при гиперболическом распределении получается гораздо больше ресурсов, чем при логарифмически нормальном. [5]
Расчет потенциалов и токов в рельсовой сети при проектировании сводится к расчету распределения указанных величин в протяженном проводнике, лежащем на поверхности земли. [6]
 |
Эквивалентная схема рельсо. [7] |
Расчет потенциалов и токов в рельсовой сети при проектировании защиты сводится к расчету распределения указанных величин в протяженном проводнике, лежащем на поверхности земли. К проводнику подключается ряд внешних нагрузок постоянного тока. [8]
Ду, , - погрешность обработки за счет колебания t3ag в партии заготовок; Ду ( Нв) - погрешность обработки, зависящая от колебания твердости материала заготовок; k - коэффициент, учитывающий отклонение закона распределения указанных величин от нормального ( см. гл. [9]
При оценке влияния корреляционной связи текущих размеров на параметры, определяющие границы регулирования процессов и индивидуальных значений xt a Jfax, x in, анализ: средних квадратических отклонений недостаточен в силу того, что величины xt имеют распределения, существенно отличающиеся от нормального. В этом случае приходится прибегать к анализу законов распределения указанных величин, получение которых обеспечивает рассмотренный выше моделирующий алгоритм. [10]
Страницы: 1