Распределение - вероятность - нахождение - электрон
Cтраница 1
Распределение вероятности нахождения электрона для атома водорода показано на рис. А. [1]
Представляет интерес установить распределение вероятности нахождения электрона на молекулярной орбитали, как это было проделано ранее для атомных орбиталей. [3]
Понятие электронного облака связано с распределением вероятности нахождения электрона в элементе объема dV около ядра. Таким образом, в отличие от самой волновой функции ее квадрат имеет физический смысл. [4]
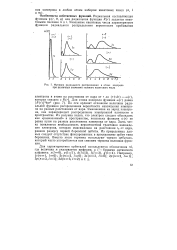 |
Функции радиального распределения в атоме водорода при различных значениях главного квантового числа. [5] |
По оси ординат отложены величины радиальной функции распределения вероятности нахождения электрона на разных расстояниях от ядра. Умноженная на заряд электрона, она характеризует распределение электронной плотности в пространстве. Из рисунка видно, что электрон следует обсуждать как размазанный в пространстве, поскольку функция ш ( г) не равна нулю на разных расстояниях электрона от ядра. Здесь четко появляется необходимость вероятностной трактовки нахождения электрона, которая максимальна на расстоянии г0 от ядра, равном радиусу первой боровской орбиты. Из приведенных данных следует отсутствие фиксированных в пространстве орбит типа боровских. Вместо этого термина используют термин орбиталь, который часто употребляется как синоним термина волновая функция. [6]
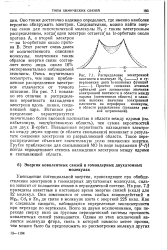 |
Распределение электронной плотности в молекуле Н2 ( - - - - - - - - и су. [7] |
На рис. 7.1 показано это отличие в распределении вероятности нахождения электрона вдоль линии, соединяющей ядра. [8]
Волновая функция %, их произведение, позволяет рассчитать распределение вероятности нахождения электрона в атоме. [9]
На рисунке 4, а приведено найденное из уравнения Шредингера распределение вероятности нахождения электрона в нормальном атоме водорода. [10]
Тот же результат можно получить, если поставить вопрос: где расположен минимум распределения вероятности нахождения электрона вблизи кулоновского центра. [11]
Волновые функции ij), представляющие собой решения волнового уравнения, связаны с распределением вероятности нахождения электрона. Предполагается, что распределение вероятности нахождения электрона передается не самой т), а произведением этой величины и комплексно-сопряженной функции. [12]
 |
Слейтеровские параметры для ванадия. [13] |
В тех случаях, когда многоэлектронный атом состоит из заполненных электронных оболочек и одного дополнительного электрона или когда ему не хватает одного электрона до завершения конфигурации, распределение вероятности нахождения электрона можно описать, используя радиальные функции по Слейтеру и одноэлек-тронные угловые волновые функции типа, приведенного в разделе Одноэлектронные волновые функции ( стр. В более сложных случаях необходимо учитывать межэлектронные взаимодействия. [14]
Волновые функции ij), представляющие собой решения волнового уравнения, связаны с распределением вероятности нахождения электрона. Предполагается, что распределение вероятности нахождения электрона передается не самой т), а произведением этой величины и комплексно-сопряженной функции. [15]
Страницы: 1 2
