Распределение - весы
Cтраница 3
Целые d и d - минимальные веса данного кода С и дуального к нему кода С соответственно, целые s и s - числа различных весов кодов С и С соответственно. Так как распределения весов кодов С и С можно вывести одно из другого на основании преобразования Мак-Вильяме ( [15], [7]), эти параметры однозначно определяются распределением весов кода С. [31]
Кодовым) расстоянием d d ( C) кода С называется минимум по всем попарным расстояниям между различными наборами из С. Ап ( х)), где А ( х) - это число векторов в С, расстояние Хэмминга от которых до ж в точности равно г. Распределение весов кода С - распределение весов этого кода по отношению к нулевому вектору. [32]
Кодовым) расстоянием d d ( C) кода С называется минимум по всем попарным расстояниям между различными наборами из С. Ап ( х)), где А ( х) - это число векторов в С, расстояние Хэмминга от которых до ж в точности равно г. Распределение весов кода С - распределение весов этого кода по отношению к нулевому вектору. [33]
Корреляционные зависимости встречаются очень часто. Например, когда мы говорим о зависимости веса человека от его роста, то речь идет, конечно, о корреляционной зависимости, так как вес не определяется ростом однозначно; в то же время ясно, что закон распределения весов двухметровых людей совсем не тот, что полутораметровых. Когда мы говорим, что курение сокращает продолжительность жизни, то, конечно, речь также идет о корреляционной зависимости, так как имеются и противоположные примеры; однако закон распределения продолжительности жизни у некурящих такой, что среднее значение этой продолжительности выше, чем у курящих. Распознание корреляционных зависимостей требует гораздо большего внимания, чем функциональных, так как на многих людей противоречащие примеры производят слишком большое впечатление. На непонимании разницы между функциональной и корреляционной зависимостями основано известное порицание. [34]
Для большинства кодов, включая и большинство БЧХ-кодов, при использовании полного алгоритма декодирования вычислить вероятность ошибки декодирования очень трудно. При таком алгоритме декодирование происходит правильно всякий раз, когда вектор ошибки является лидером смежного класса. Для большинства кодов распределение весов лидеров смежных классов мало изучено. С неконструктивной точки зрения последняя задача больше поддается решению. Оказывается, скорее можно построить точную верхнюю границу для вероятности ошибки наилучшего кода, чем найти такой код. [35]
Кроме параметра скорости кода Rc, важным параметром кодового слова является его вес, который равен числу ненулевых элементов, слова. В общем, каждое кодовое слово имеет свой собственный вес. Набор всех весов кода образует распределение весов кода. Когда все М кодовых слов имеет одинаковый вес, код называется кодом с фиксированным весом или кодом с постоянным весом. Функции кодирования и декодирования включают арифметические операции суммирования и умножения, выполненные над кодовыми словами. Эти арифметические операции выполняются в соответствии с соотношениями, правилами для алгебраического поля, которое имеет своими элементами символы, содержащиеся в алфавите кода. Для примера, символы в двоичном алфавите равны 0 и 1; следовательно, поле имеет два элемента. [36]
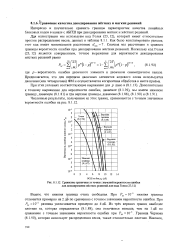 |
Сравнение граничных и точных значений вероятности ошибки для декодирования жестких решений для кода Голея ( 23 12. [37] |
Видим, что нижняя граница очень свободная. При Рм - 10 - 5 нижняя граница отличается примерно на 2 дБ по сравнению с точным значением вероятности ошибки. Граница Чернова (8.1.90), которая использует распределения весов, также относительно плотная. [38]
На основании распределения расстояний произвольного кода и его преобразования Мак-Вильяме определяются четыре параметра кода, которые в линейном случае сводятся к минимальному весу и числу различных весов данного кода и дуального к нему. В общем случае выясняется комбинаторный смысл этих параметров и с помощью их получаются различные результаты относительно метрических свойств кода. В частности, предложен метод вычисления распределения весов классов смежности кода. Кроме того, представлено и подробно исследовано дуальное понятие для совершенного кода. [39]
 |
Деление нейрона с максимальной ошибкой в растущем нейронном газе. [40] |
Соревновательные слои нейронов широко используются для квантования данных ( vector quantization), отличающегося от кластеризации лишь большим числом прототипов. Это весьма распространенный на практике метод сжатия данных. При достаточно большом числе прототипов, плотность распределения весов соревновательного слоя хорошо аппроксимирует реальную плотность распределения многомерных входных векторов. Входное пространство разбивается на ячейки, содержащие вектора, относящиеся к одному и тому же прототипу. [41]
Если код С не является линейным, то понятие дуального кода С не определено. Дельсарт показал [30], что если вычислить формально распределение весов А ( С) через тождества Мак-Вильяме и положить d равным минимальному натуральному г, такому что Ai ( C -) Q, то максимальная сила ОА, соответствующего коду С будет равна d - l так же, как и для линейного кода. [42]
К сожалению, нумератор весов не дает полной информац) которую нам бы хотелось иметь о коде. Например, он ничего говорит о вероятности ошибки декодирования при использова. В частности, суженный дво: ный КВ-код с длиной 31 и 2-укороченный РМ-код второго поря; с длиной 31 имеют один и тот же нумератор весов, хотя, как пока; вает задача 15.1, распределения весов лидеров смежных клас у этих кодов различны. [43]
Страницы: 1 2 3