Распределение - сила - трение
Cтраница 2
При решении задач теории обработки металлов давлением возникает необходимость в математическом представлении функции распределения сил трения по контактной поверхности. [16]
Для выяснения динамических нагрузок на опоры аппарата необходимо учесть ряд особенностей в характере распределения сил трения и инерционных сил в зависимости от способа подключения пульсатора к аппарату. Так как характер усилий, возникающих при пульсации, не зависит от типа генератора импульсов, то последующие рассуждения для наглядности будем вести для поршневого пульсатора, обеспечивающего синусоидальную форму колебаний. [17]
 |
Зона прилипания и распределение сил трения по контактной поверхности при осадке. [18] |
Оценка возможности возникновения зоны прилипания и определение ее размеров являются важнейшими условиями правильного анализа распределения сил трения по контактной поверхности. [19]
Приведены материалы по определению сил внешнего трения в различных процессах обработки металлов давлением, эпюры распределения сил трения на контактной поверхности, данные по коэффициенту трения для конкретных условий обработки. Освещены методы определения коэффициента трения в процессах пластического деформирования. Рассмотрены вопросы теории смазочного действия, сортамент эффективных технологических смазок, способы их производства, а также смазочные системы и условия их эксплуатации. Описаны методы испытания смазочных веществ. Даны технико-экономические показатели смазок. [20]
Определить условия срыва жидкости путем теоретического анализа не представляется возможным, так как мы не располагаем данными о распределении силы трения газа по поверхности водны, и точное решение уравнений волнового движения соп-ряжено с большими трудностями. Сравнение имеющихся зависимостей показывает, что по степени влияния физических свойств жидкости и газа и учитываемых факторов формулы существенно отличаются друг от друга. [21]
Определить условия срыва жидкости путем теоретического анализа не представляется возможным, так как мы не располагаем данными о распределении силы трения газа по поверхности волны и точное решение уравнении волнового движения сопряжено с большими трудностями. [22]
Уравнения ( 3 - 6) редко могут быть использованы в практике, в частности, потому, что распределение сил трения в реальных потоках ( особенно при так называемом резкоизменяющемся движении жидкости) учесть весьма трудно. [23]
Так как распределение сил трения является практически неизвестным, а известен только интегральный эффект действия сил трения, то можно принять любую гипотезу о распределении сил трения, эффект действия которых эквивалентен интегральному эффекту. [24]
Рассматривая третий этап, соответствующий увеличению нагрузки после разгрузки, нетрудно заметить, что у конца полосы на некоторой длине as вновь возникнут положительные смещения; распределение сил трения для этого этапа показано на фиг. [25]
Так как распределение сил трения практически неизвестно, а известен ( экспериментально) только интегральный эффект действия сил трения, то можно принять любую гипотезу о распределении сил трения, эффект действия которых эквивалентен интегральному эффекту. Поэтому естественно предположить, что сила трения распределена так, что выполняется условие (6.114), т.е. главные координаты для консервативной системы остаются главными и для неконсервативной системы, учитьшающей силы вязкого трения. [26]
Компоненту Ry называют поперечной силой; в тяжелой жидкости она слагается из трех сил: силы Архимеда Ау ( см. § 13), направленной по вертикали вверх и не зависящей от скорости потока, силы трения Ryt, определяемой вторым интегралом (44.2) и зависящей от распределения сил трения по поверхности тела, и вертикальной слагающей Y силы Rv ( см. § 31); направление этой слагающей зависит от направления циркуляции вектора скорости и может совпадать с направлением архимедовой силы или быть противоположно ей. [27]
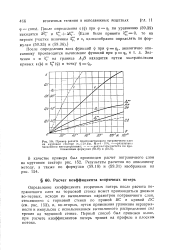 |
Пример расчета пространственного пограничного слоя. [28] |
Определение коэффициента вторичных потерь после расчета пограничного слоя на торцовой стенке может производиться двояко: во-первых, исходя из вычисленных параметров пограничного слоя, стекающего с торцовой стенки по прямой ВС и кривой DC ( см. рис. 153), и, во-вторых, путем применения уравнения неразрывности и импульсов с использованием вычисленного распределения сил трения на торцовой стенке. Первый способ был применен выше, при расчете коэффициентов потерь трения на профиле в плоском потоке. [29]
Сначала силы трения препятствуют соскальзыванию груза под действием силы тяжести. Полный расчет распределения сил трения, действующих на веревку, довольно сложен, поскольку сила натяжения веревки в местах ее соприкосновения с бревном меняется от F, до тд. В свою очередь сила давления веревки на бревно также меняется, будучи пропорциональной в каждой точке соответствующей локальной силе натяжения веревки. Соответственно и силы трения, действующие на веревку, определяются именно указанными силами давления. [30]
Страницы: 1 2 3