Распределение - внутренняя сила
Cтраница 2
Чтобы характеризовать закон распределения внутренних сил по сечению, необходимо ввести для них числовую меру. За такую меру принимается напряжение. [16]
Так как закон распределения внутренних сил по сечению не известен, то следует воспользоваться правилами статики и привести систему внутренних сил к центру тяжести сечения. [17]
Чтобы характеризовать закон распределения внутренних сил по сечению, необходимо ввести для них числовую меру. За такую меру принимается напряжение. [18]
Это существенно влияет на законы распределения внутренних сил п напряженном теле, хотя само по себе изменение формы является, как правило, незначительным и обнаруживается в большинстве случаев только при помощи чувствительных инструментов. [19]
Это существенно влияет на законы распределения внутренних сил в напряженном теле, хотя само по себе изменение формы является, как правило, незначительным и обнаруживается в большинстве случаев только при помощи чувствительных инструментов. [20]
Метод сечений не позволяет установить закон распределения внутренних сил по сечению. Необходимы дополнительные допущения о характере деформаций. Эти допущения вводят при изучении различных видов деформаций бруса. [21]
Метод сечений не позволяет определить аакон распределения внутренних сил по сечению. Для этого необходимы дополнительные допущения о характере деформаций, рассматриваемые в соответствующих разделах. [22]
Метод сечений не позволяет определить закон распределения внутренних сил по сечению. Для этого необходимы дополнительные допущения о характере деформаций. Эти допущения вводятся при изучении различных видов деформаций. [23]
Известно, что в статически неопределимых системах распределение внутренних сил зависит от упругих свойств элементов системы, вследствие чего одних уравнений равновесия оказывается недостаточно для определения всех усилий в конструкции. В общем случае уравнения статики должны решаться совместно с физическими и геометрическими уравнениями, выражающими условия деформации системы. Для упрощения обычно расчет строится таким образом, что какие-то факторы системы выбираются в качестве основных неизвестных, которые должны вполне определять ее напряженно-деформированное состояние. Это значит, что через основные неизвестные должно быть возможно выразить все прочие интересующие нас величины в конструкции. [24]
 |
Сплошные железобетонные фундаменты. [25] |
При учете взаимодействия сооружения с фундаментами выясняется более достоверное распределение внутренних сил в конструктивных элементах сооружения и достигается существенная экономия строительных материалов. [26]
При контурных конструкциях в виде ферм характер распределения внутренних сил в фермах существенно изменяется. Из условия равновесия сил на ферме - сумма моментов относительно опоры В при силах Nxy, приложенных по оси верхнего пояса равна нулю ( см. рис. 14.26, в) - находят, что реакция опоры А равна нулю. Следовательно, равномерно распределенная нагрузка покрытия по схеме на рис. 14.26, б воспринимается только двумя опорами В и D, опоры Л и С не загружены. Нижний пояс и все элементы решетки фермы не напряжены. [27]
Во всяком случае, приближенное решение задачи о распределении внутренних сил в стержнях фермы, найденное на основании трех приведенных выше предположений, в большинстве случаев может найти практическое применение при технических расчетах элементов фермы на прочность. [28]
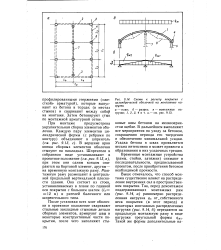 |
Схемы к расчету покрытия с цилиндрической оболочкой на монтажные нагрузки. [29] |
Выше отмечалось, что способ монтажа существенно влияет на распределение внутренних сил в пространственном покрытии. [30]
Страницы: 1 2 3 4