Распределение - температура - стенка
Cтраница 1
Распределение температуры стенки по длине и радиусу теплообменного аппарата с витыми трубами можно определить, используя различные методы расчета пограничного слоя при заданном внешнем течении, которое рассчитывается при решении системы уравнений, описывающих течение гомогенизированной среды. Это могут быть численные методы расчета либо методы, основанные на приближенной замене исходной системы двумерных уравнений системой одномерных уравнений. Последние методы являются в ряде случаев более простыми и удобными, поскольку для их уточнения можно использовать опытные данные по коэффициентам теплоотдачи и гидравлического сопротивления, полям скорости и температуры. В этом методе одномерные уравнения решаются с использованием быстро сходящихся последовательных приближений. [1]
Распределение температуры стенки tCT по высоте аппарата имеет сложный характер: в нижней части теплообменной поверхности наблюдается значительное изменение tCT, затем оно происходит медленнее и температура остается постоянной в верхней части поверхности. [2]
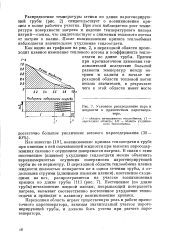 |
Условное распределение пара и жидкости в прямоточном парогенераторе. [3] |
Распределение температуры стенки по длине парогенерирую-щей трубы ( рис. 2) свидетельствует о возникновении кризиса в конце рабочего участка. При этом наблюдается рост температуры поверхности нагрева и падение температурного напора натрий-стенка, что свидетельствует о снижении теплового потока от натрия к калию. После возникновения кризиса теплообмена наблюдается значительное ухудшение теплоотдачи. [4]
 |
Заделка горячего спая. [5] |
Зная характер распределения температур стенки и жидкости по длине экспериментального участка и количество конденсату с выделенных участков кипятильной трубы, можно легко определить локальные тепловые потоки и температурные напоры и затем по общеизвестной формуле рассчитать локальные коэффициенты теплоотдачи. [6]
Для каждого режима строятся графики распределения температуры стенки и температуры жидкого металла по длине трубы. [7]
Для каждого режима строятся графики распределения температуры стенки и температуры жидкого металла по длине трубы. Осредненная линия проводится по показаниям 13 - 20 термопар в зависимости от длины обогреваемого участка. На основной обогреваемой части температуры стенки и жидкого металла имеют линейный характер изменения. На концах обогреваемого участка температура стенки постепенно переходит к постоянным значениям, которые соответствуют температурам жидкого металла перед началом обогреваемого участка и после него. Измерения распределения температур по поперечному сечению потока показывают, что длина участка тепловой стабилизации составляет всего 2 - 7 7 диаметров. Местные значения коэффициентов теплоотдачи вычисляются по уравнению ( 5 - 6) для трех сечений. Тепловой поток определяется по массовому расходу натрия и изменению его температуры. Он сопоставляется с тепловым потоком, найденным по мощности, потребляемой соответствующими электрическими нагревателями, за вычетом потерь тепла в окружающую среду. Температура стенки в расчетных сечениях трубы определяется из графиков, построенных по данным опыта, с учетом поправки на перепад температуры в стенке трубы на глубине заделки горячего спая термопар. [8]
Изменения скорости в пограничном слое и распределения температуры стенки свидетельствуют о том, что пограничный слой действительно становится турбулентным в точке, расположенной на расстоянии 327 8 мм от передней кромки или даже ближе. [9]
Решение для произвольного, но известного закона распределения температуры стенки Tw () может быть получено путем суммирования решений для соответствующего распределения указанных выше приращений температуры стенки. Влияния на теплообмен при фиксированном значении х каждого приращения температуры стенки dTe при учитываются дополнительным введением интеграла Стилтьеса. [10]
Относительно функции tp ( - X), описывающей распределение температуры стенки по длине трубы, предполагается, что она больше нуля при QXoo и непрерывна вместе со своими производными. [11]
Система уравнений (2.21), (2.22) и (2.23) полностью характеризует распределение температур стенки трубы и потока жидкости и позволяют численными методами производить расчеты температурных полей неконтактных термоконвективных преобразователей. [12]
Обычно в таком расчете задаются геометрией проточной части сопла, распределением температуры стенки и начальными параметрами газа. [13]
Таким образом, для определения местных коэффициентов теплоотдачи в рассматриваемом случае течения необходимо было измерить распределения температуры стенок витых тРУб, удельного теплового потока, температуры теплоносителя и скорости потока вне пристенного слоя по радиусу пучка в данном поперечном сечении. Экспериментальные поля температуры теплоносителя и скорости потока в поперечном сечении пучка хорошо согласуются с расчетными полями температуры и скорости, определенными для гомогенизированной модели течения. [14]
При расчете систем охлаждения различных технических устройств часто встречается задача совместного решения системы одномерных уравнений, описывающих распределения температур стенки и жидкости по длине канала. Рассмотрим наиболее простой вариант этой задачи. [15]
Страницы: 1 2 3 4