Распределение - фишер
Cтраница 3
Величина F при условии справедливости нулевой гипотезы имеет распределение Фишера - Снедекора ( см. гл. XII, § 15) со степенями свободы k1 - n1 - 1 и Й2 п2 - 1, где t - объем выборки, по которой вычислена большая исправленная дисперсия, 2 - объем выборки, по которой найдена меньшая дисперсия. Напомним, что распределение Фишера - Снедекора зависит только от чисел степеней свободы и не зависит от других параметров. [31]
Представлены результаты исследования пористости фильтрующих патронов в зависимости от их состава. Использован статистический метод анализа распределения пористости и дана методика расчета. Показано что квантиль распределения Фишера при доверительной вероятности 0 95 меньше расчетного критерия и, следовательно, влияние фактора, учитывающего состав патронов, является значимым. [32]
Такого рода характеристика явлений, влияющих на уровень и динамику валютного курса, является непременным этапом, предшествующим самостоятельному статистическому анализу факторов на основе конкретного цифрового материала. Напомним, что выбор функции осуществляется исходя из показателей значимости уравнения и ошибок аппроксимации. Для проверки значимости используют F-критерий с распределением Фишера. [33]
Другой метод заключается в подборе линии регрессии, являющейся эмпирической оценкой функции влияния некоторой величины W, на результат наблюдения. Оценку находят, группируя в серии данные наблюдений при близких значениях влияющей величины. Для отношения межсерийной и внутрисерийной дисперсии принимают распределение Фишера и при соответствии этого отношения доверительному интервалу находят джПерсии параметров ливни регрессии. [34]
Таким образом, избыток галоидного алкила не влияет на выход полимера. Незначимый эффект в табл. 52 заменен нулем. Для оценки значимости эффектов в дисперсионном анализе было использовано отношение средних квадратов, обусловленных действием соответствующих факторов к среднему квадрату, связанному с ошибкой опыта, имеющее распределение Фишера. [35]
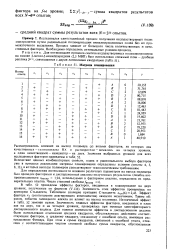 |
Матрица планирования. [36] |
Таким образом, избыток галоидного алкила не влияет на выход полимера. Незначимый эффект в табл. 52 заменен нулем. Для оценки значимости эффектов в дисперсионном анализе было использовано отношение средних квадратов, обусловленных действием соответствующих факторов, к среднему квадрату, связанному с ошибкой опыта, имеющее распределение Фишера. [37]
Таким образом, избыток галоидного алкила не влияет на выход, полимера. Незначимый эффект в табл. 52 заменен нулем. Для оценки значимости эффектов в дисперсионном анализе было использовано отношение средних квадратов, обусловленных действием соответствующих факторов к среднему квадрату, связанному с ошибкой опыта, имеющее распределение Фишера. При этом к сумме квадратов, связанной с ошибкой опыта, отнесена с срответст-вующим числом степеней свободы сумма квадратов, обусловленная действием фактора х %, эффект которого оказался незначимым. Данные факторного и дисперсионного анализов хорошо согласуются. [38]
Анализ полученных результатов показывает, что существует зависимость между выбранными показателем эффективности виброволнового воздействия и геолого-технологическими факторами. При этом также наблюдается существенная корреляция между факторами процесса, т.е. данные обладают свойствами мультиколлинеарности. Это затрудняет проведение анализа и определение коэффициентов корреляционных моделей. Трудно установить, какие факторы влияют наиболее существенно и определить степень этого влияния. В результате регрессионного анализа получена линейная зависимость, прогнозирующая показатель при заданных значениях факторов. Критериями надежности данной модели являются мера идентичности и коэффициент множественной корреляции, характеризующие часть дисперсии показателя, которую описывает данная регрессия, F - отношение, характеризующее меру надежности данного выражения ( в сравнении с проценти-лями распределения Фишера), оценка несмещенности и доверительные интервалы ( вычисленные с помощью распределения Стьюдента), характеризующие ошибки предсказания. [39]
Страницы: 1 2 3