Распределение - число - молекула
Cтраница 1
Распределение числа молекул по скоростям согласно уравнению Максвелла является формой равновесия теплового движения. [1]
 |
Энергетические уровни в молекулярной системе. [2] |
При тепловом равновесии распределение числа молекул на энергетических уровнях выражается экспоненциальным законом Больцмана. [3]
В газовой смеси существует распределение числа молекул по значениям их энергии по закону Максвелла - Больцмана. В реакции участвуют молекулы, энергия которых превышает некоторую величину, - активные молекулы. Следует различать два случая: а) скорость реакции сравнительно мала, а потому убыль числа активных молекул успевает компенсироваться соударениями молекул. Такие реакции стационарны относительно максвелл-больцмановского распределения. [4]
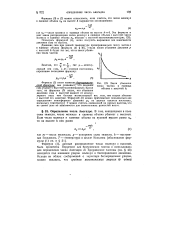 |
Закон убывания. [5] |
Формула ( 1), дающая распределение числа молекул с высотой, была применена Перреном для броуновских частиц и использована для определения числа Авогадро N. Броуновские частицы ( см. § 43) находятся под влиянием ударов молекул в беспорядочном движении. [6]
Чтобы подсчитать полное изменение, вносимое в распределение числа молекул происходящими столкновениями, необходимо рассмотреть все такие столкновения, где первая молекула есть какая-нибудь a - молекула, тогда как другая имеет любое направление линии центров при ударе и любую скорость. При подсчете обратных столкновений надо выбирать только такие, у которых после столкновения одна молекула имеет любую скорость и направление линии центров, а другая имеет скорость a - молекулы. [7]
Для определения спектрального распределения интенсивности ультрафиолетового излучения различных источников света производится распределение числа молекул разложившейся щавелевой кислоты для урани-локсалатного актинометра или числа ионов железа для ферриоксалатного актинометра пропорционально относительной энергии излучения для узких интервалов длин волн спектров излучения ламп. [8]
Допущение Гриффитса о том, что распределение молекул в частицах в зависимости от размеров этих частиц аналогично распределению числа молекул по их энергии, имеющему место в кинетической теории газов, не обосновано и мало вероятно. Более вероятным представляется допущение Фаренволда и Загустина о применимости к процессу дробления закона Максвелла ( см. стр. Однако применение полученных Загустиным функциональных зависимостей затруднительно, вследствие чего они не получили распространения в практике. [9]
Очевидно, что отношение ДЛ / / Да показывает, сколько молекул приходится на каждый единичный интервал скорости, иными словами, каково распределение числа молекул по скоростям; ДЛ / / Д v зависит от скорости и называется функцией распределения числа молекул по скоростям. [10]
Очевидно, что отношение ДЛ / / Да показывает, сколько молекул приходится на каждый единичный интервал скорости, иными словами, каково распределение числа молекул по скоростям; ДЛ / / Д v зависит от скорости и называется функцией распределения числа молекул по скоростям. [11]
Таким образом, уравнения (IX.9) и (IX.10) позволяют выразить долю вертикально двигающихся молекул в данном объеме газа, которые имеют скорости, лежащие в пределах от и до и А. Задавая различные значения и, можно таким путем найти распределение чисел молекул по скоростям. Мы рассмотрели вертикальное движение молекул газа, однако полученные результаты справедливы для движения в любых направлениях. [12]
Величины Г и W не зависят от того, какие именно молекулы находятся в одной, а какие в другой части сосуда. Однако фактически представляет - интерес не распределение каких-то определенных молекул, а просто распределение числа молекул по обеим частям сосуда. [13]
И в исследования включается Больцман. Уже в 21 год он пишет свою первую работу на эту тему под названием Механический смысл второго начала. В 1868 - 1871 гг. Больцман распространяет доказательство Максвелла на газы, находящиеся во внешнем силовом поле, например гравитационном поле Земли, когда на каждую молекулу действует еще сила тяжести. С учетом этого Больцман устанавливает новый закон - закон распределения числа молекул по энергиям, выведя выражение соответствующей функции. Последнее ясно показывает противоположное действие сил гравитации, стремящихся удержать молекулы на дне сосуда, и сил тепловых столкновений молекул, поднимающих их вверх. [14]
Страницы: 1