Распределение - время - безотказная работа
Cтраница 1
Распределение времени безотказной работы представляет существенный интерес при решении ряда практических вопросов. Сюда относятся вопросы контроля качества продукции, расчета межоперационных запасов и ряд других. Поэтому необходимо изучить теоретические схемы возникновения неисправностей и соответствующие им распределения времени безотказной работы. [1]
Распределение времени безотказной работы сложных систем в большом числе случаев можно аппроксимировать экспоненциальным распределением, поэтому рассмотрим случай показательного распределения. Предположим, что проверки производят через каждые х единиц времени. [2]
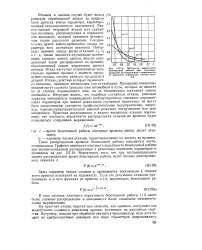 |
Плотность вероятности безотказной работы при экспоненциальном распределении в зависимости от величины параметров потока отказов. [3] |
Такое распределение времени безотказной работы называется экспоненциальным. [4]
Отклонения распределения времени безотказной работы от экспоненциального происходят в основном по двум причинам: 1) преобладают ранние отказы из-за элементов со скрытыми дефектами, не обнаруженными во время выходного контроля производства и тренировки; 2) преобладают поздние отказы из-за постепенного износа деталей, накапливаемого разрушения, усталости и пр. На участке старения система имеет возрастающую со временем интенсивность отказов. Как показано в [21], при высокой однородности качества изделий модель с постоянной средней скоростью износа и накоплением разрушений приводит к гамма-распределению с целочисленным параметром &1. Именно такое распределение наблюдается в системе при последовательном соединении элементов, имеющих гамма-распределение времени безотказной работы, параметры которого несколько изменяются от элемента к элементу. [5]
Закон распределения времени безотказной работы хроматографа - экспоненциальный. [6]
Требуется исследовать распределение времени тк безотказной работы устройства. [7]
Экспоненциальный закон распределения времени безотказной работы применим к механизмам, прошедшим предварительную приработку. Этот вид распределения используется также при анализе внезапных отказов. [8]
Если закон распределения времени безотказной работы известен по предшествующей аппаратуре, то табл. 30 - 12 дает достаточную исходную информацию для определения показателей безотказности. Подобную же таблицу необходимо иметь и для определения показателей ремонтопригодности. [9]
Если закон распределения времени безотказной работы данной аппаратуры - по опыту эксплуатации предшествующей аппаратуры не был определен, то табл. 5 - 10 дает достаточную исходную информацию, чтобы наряду с показателями безотказности аппаратуры найти и закон распределения. Подобную же таблицу необходимо иметь и для определения показателей ремонтопригодности. [10]
Требуется выявить закон распределения времени безотказной работы. [11]
Анализ кривых плотностей распределения времени безотказной работы насосов показал, что отказы насосов по причине износа рабочих колес, изготовленных из стали 20Х13Л, начинают появляться уже после IOOO-IIOO часов, в то время как для насосов с рабочими колесами из стали XI7H2I они появляются лишь после 2000 - 3000 часов работы насосов. [12]
Для выявления закона распределения времени безотказной работы подшипникового узла, составим табл. 1 [35], в которой введены следующие обозначения: xt - вариационный ряд наработок между отказами; n - L - наблюдаемые числа появления наработок между отказами; Я, - суммы частот наработок; п - число опытов. [13]
Выше указывалось, что распределение времени безотказной работы устройств обычно подчиняется экспоненциальному закону. [14]
Экспоненциальный закон хорошо описывает распределение времени безотказной работы объектов при внезапных отказах, распределение времени между соседними отказами и времени восстановления. Для объектов, у которых явно выражены при эксплуатации явления износа и старения, применение1 экспоненциального закона недопустимо. [15]
Страницы: 1 2 3 4