Распределение - время - безотказная работа - элемент
Cтраница 1
 |
Расчет показателей надежности. [1] |
Распределение времени безотказной работы элементов подчинено экспоненциальному закону. [2]
При доказательном распределении времени безотказной работы элементов поток отказов является простейшим: стационарным, ординарным и без последействия. [3]
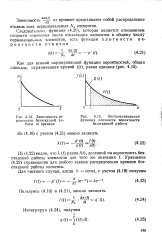 |
Зависимость вероятности безотказной работы от времени. [4] |
Уравнение (4.22) справедливо для любого закона распределения времени безотказной работы элемента. [5]
Обозначим: F ( x) - функцию распределения времени безотказной работы элемента; FT ( x) - г-крат-ную свертку F ( x); Nt - число отказов в интервале ( 0, t) в единичном процессе восстановления; Zr - сумму г независимых значений времени безотказной работы. [6]
К нестационарности и последействию в потоке может привести отличие законов распределения времени безотказной работы элементов от экспоненциального. Такое отличие по-разному сказывается на свойствах потока в зависимости от сложности и состава аппаратуры и вида отказа. [7]
 |
График вероятностей. [8] |
Вид выражения зависит от продолжительности интервалов Т, от законов распределения времени безотказной работы элементов системы, от вероятностей их использования и от средних значений продолжительности их нерабочих периодов. [9]
Уже по виду формулы ( 1 - 15) можно заключить, что вычисление функции надежности системы по плотностям распределения времени безотказной работы элементов в общем случае приводит к очень громоздким вычислениям. [10]
Пусть для определенности период времени Т постоянен, а интенсивность отказов - возрастающая функция времени, причем F ( t) - распределение времени безотказной работы элемента. Оценим среднее время работы элемента до отказа с учетом замен. [11]
Если эксплуатация и профилактическое обслуживание систем управления организованы надлежащим образом, то потоки отказов элементов действительно близки к простейшим. Это позволяет практически всегда использовать в качестве модели распределений времени безотказной работы элементов систем управления экспоненциальное распределение, полной и удобной характеристикой которого является интенсивность отказов А, имеющая постоянную величину. [12]
Априорный анализ надежности предполагает использование гипотетических математических моделей, отражающих вероятностные процессы функционирования исследуемых реальных устройств. В первую очередь это относится к математическим моделям последовательностей отказов и восстановлений - моделям распределений времени безотказной работы элементов, времени работы между отказами и времени восстановления систем. [13]
Оптимизация достигается варьированием сроков и объемов профилактических работ. Профилактики заключаются в принудительной замене элементов, возраст которых достиг определенной величины, причем сроки замены назначаются на основании априорной информации о распределении времени безотказной работы элементов системы. Описываются системы, у которых можно выделить ряд промежуточных состояний, позволяющих судить о степени приближения системы к отказу. Для таких систем профилактика проводится по достижении системой некоторого критического состояния. [14]
На этапах эскизного и технического проектирования систем применяются инженерные методы анализа и расчета надежности. Цель расчета - определение показателей надежности системы и разработка мероприятий по ее повышению, в результате чего должен быть обеспечен ее необходимый уровень. На стадии проектирования отсутствуют экспериментальные статистические данные, которые могут быть получены при испытаниях и эксплуатации системы. Поэтому для анализа надежности используют априорную информацию и гипотетические математические модели, отражающие вероятностные процессы функционирования исследуемых реальных систем. Обычно рассматриваются математические модели распределения времени безотказной работы элементов, времени работы между отказами и времени восстановления систем. [15]
Страницы: 1