Частотно-угловое распределение
Cтраница 1
Частотно-угловое распределение для регулярной стопки имеет сильно осцилляционный характер и поэтому не приведено на рисунках. [2]
Частотно-угловое распределение интенсивности полного излучения определяется формулой (16.1), где величина В слагается из вкладов от обеих пластин и трех вакуумных участков. [3]
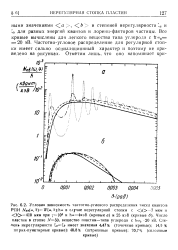
Были получены формулы для частотно-угловых распределений интенсивностей излучения разных поляризаций. Из анализа этих формул, в частности, следует, что переходное излучение в оптической области частот имеет максимумы в направлениях, определяемых из геометрической оптики ( с точностью до угла порядка т 1) - В области же рентгеновских и более высоких частот все излучение в основном сосредоточено вдоль траектории заряженной частицы. [4]
Когда ХСт 2CU B частотно-угловом распределении интенсивности излучения возникает максимум. При этом анализ формул показывает, что если вся стопка достаточно прозрачная, то интенсивность максимума будет пропорциональна квадрату числа пластин в стопке Л / 2, а ширина максимума будет меньше примерно в Л / раз. В результате полная интенсивность ( или число квантов), проинтегрированная по всему максимуму, будет больше примерно в Л; раз. Аналогичный результат получается и в том случае, когда стопка недостаточно прозрачная. Тогда полная интенсивность ( или полное число квантов) максимума оказывается больше в соответствующее число Л7эфф раз. [5]
Подставляя (6.18) в (6.9), получаем формулу для частотно-углового распределения интенсивности РПИ, образованного в пластине со случайной толщиной. [6]
В случае нерегулярной стопки пластин имеет место сглаживание частотно-углового распределения интенсивности переходного излучения. Если отношения средних квадратичных отклонений толщин пластин и расстояний между пластинами к соответствующим квадратам зон формирования намного меньше N - l ( см. (6.17)), то частотно-угловое распределение интенсивности излучения мало отличается от соответствующего распределения для регулярной стопки. Если же среднее квадратичное отклонение расстояний между пластинами ( и толщин пластин) намного больше квадратов соответствующих зон формирования, то происходит независимое сложение интенсивностей от N пластин ( и соответственно 2N границ) с учетом, естественно, поглощения излучения в среде. [7]
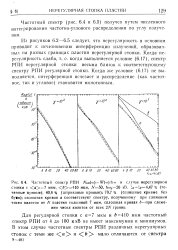
Ян Ши [73.3, 74.4] впервые была получена и проанализирована общая формула для частотно-углового распределения усредненной интенсивности РПИ, образуемого в произвольной нерегулярной стопке ( и не имеющего при достаточно большой нерегулярности резонансного характера), а также были рассчитаны соответствующие частотные спектры. [8]
Частотный спектр ( рис. 6.4 и 6.5) получен путем численного интегрирования частотно-углового распределения по углу излучения. [10]
При выполнении этого условия нерегулярная стопка мало отличается от регулярной с точки зрения частотно-углового распределения РПИ. [11]
С помощью формул (6.33), (6.34) и аналогичных формул для Aft, Qb совместно с формулами (6.6) и (6.9) можно вычислить частотно-угловое распределение интенсивности РПИ, образуемого в нерегулярной стопке. [12]
Если при этом средний квадрат угла многократного рассеяния на длине а все же меньше квадрата угла излучения л - ( т.е. имеет место условие ( 16 32)) то можно показать, что выражение (16.37) сводится ( для Ног; 2) к формуле для частотно-углового распределения обычного переходного излучения, образуемого в пластине. [13]
В случае пластины происходит интерференция излучений, образованных на разных границах. Когда толщина а пластины намного больше зоны формирования переходного излучения 2веш ( й) ( см. (2.25)), интерференционные максимумы и минимумы в частотно-угловом распределении интенсивности расположены очень близко друг от друга, так что после усреднения по небольшому интервалу углов ( или частот) имеет место как бы независимое сложение интенсивностей ( чисел квантов) излучений, образованных на отдельных границах. [14]
В случае нерегулярной стопки пластин имеет место сглаживание частотно-углового распределения интенсивности переходного излучения. Если отношения средних квадратичных отклонений толщин пластин и расстояний между пластинами к соответствующим квадратам зон формирования намного меньше N - l ( см. (6.17)), то частотно-угловое распределение интенсивности излучения мало отличается от соответствующего распределения для регулярной стопки. Если же среднее квадратичное отклонение расстояний между пластинами ( и толщин пластин) намного больше квадратов соответствующих зон формирования, то происходит независимое сложение интенсивностей от N пластин ( и соответственно 2N границ) с учетом, естественно, поглощения излучения в среде. [15]
Страницы: 1