Теоретическое распределение - вероятность
Cтраница 1
Теоретическое распределение вероятностей переходит при Д - 0 в гладкую кривую. Функцию р ( х) называют плотностью вероятности. [1]
Существование теоретического распределения вероятностей является основополагающим предположением теории ошибок, которое, строго говоря, нельзя проверить экспериментально. [2]
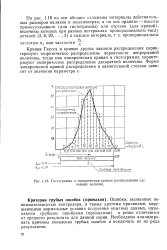 |
Гистограмма и эмпирическая кривая распределения случайных величин. [3] |
Кривая Гаусса и кривые других законов распределения характеризуют теоретическое распределение вероятности непрерывной величины, тогда как эмпирическая кривая и гистограмма характеризуют эмпирическое распределение дискретной величины. [4]
КРИТЕРИЙ НА-КНАДРАТ - ста тистический критерий, используемый для определения близости теоретического распределения вероятностей к наблюденному распределению частот. Иногда используется как одна из мер силы связи или критерий интенсивности ориентировки. В последнем случае применяется условно. [5]
Примерами концептуального подхода являются модели распределения химического элемента в горных породах, построенные А. Б. Вистелиусом, Д. А. Родионовым и др. С иными подходами к процедуре выбора теоретического распределения вероятностей ( механическая, физическая и другие модели) можно познакомиться в работах Дж. Общим условием использования теоретической плотности распределения для решения указанных выше задач является достаточно хорошая согласованность выбранной плотности распределения с эмпирически наблюдаемым частотным распределением. Следует, однако, помнить, что выборочные данные могут удовлетворять сразу нескольким плотностям распределения вероятностей, в связи с чем принятие того или иного конкретного закона распределения в качестве вероятностной модели изучаемого природного явления почти всегда гипотетично. С другой стороны, имеются определенные трудности в проверке согласованности теоретической плотности распределения, выбранной на основании вневероятностных соображений ( например, при физико-химическом анализе явления), и эмпирического частотного распределения. Дело в том, что выборочные данные, как правило, отягощены различного рода методическими погрешностями. Последние могут существенно искажать исходное распределение. Еще одна сложность связана с возможной статистической неоднородностью исследуемого объекта, что может, как и в предыдущем случае, приводить к появлению смешанных распределений. [6]
Мы видели, что эмпирическое распределение часто-стей и соответствующее ему теоретическое распределение вероятностей могут быть заданы в виде таблиц или кумулятивных функций распределения. Отсюда мы получаем наиболее полную, хотя иногда и трудно обозримую информацию о поведении случайной величины в ходе испытаний. [7]
Эта задача сводится к тому, чтобы по известному распределению эмпирических частот появления случайной величины определить соответствующее ему теоретическое распределение вероятностей. [8]
Когда п возрастает, многие статистики сходятся по вероятности к соответствующим параметрам теоретического распределения X. В частности, относительные частоты сходятся в среднем к соответствующим вероятностям. Поэтому каждую выборку рассматривают как выборку из теоретически бесконечной генеральной совокупности, в которой распределение признака совпадает с теоретическим распределением вероятностей величины X. Последнее называется распределением генеральной совокупности, а его параметры - параметрами генеральной совокупности. Во многих приложениях теоретическая генеральная совокупность есть только полезная идеализация действительной совокупности, из которой получена выборка. [9]
Изменения направления траектории заряженной частицы, движущейся в материальной среде, обусловлены ее взаимодействиями с электрическими полями атомов, через которые проходит частица. Эти взаимодействия зависят от заряда, скорости и импульса частицы, так что измерение изменений направления является источником информации о массе и энергии заряженной частицы. Поскольку измерения многократного рассеяния проводятся путем определения отклонений на траектории частицы при ее прохождении через конечную толщину материала, необходимо рассмотреть три различных вопроса: теоретическое дифференциальное сечение для индивидуальных актов рассеяния; статистическую комбинацию последовательных одиночных актов для вычисления теоретического распределения вероятностей отклонения; интерпретацию статистически малого числа измерений в связи с этой теоретической функцией распределения. [10]
Как было указано во введении, одной из основных задач математической статистики является реконструкция теоретического закона распределения генеральной совокупности по данным эмпирического распределения выборки. В случае одномерной совокупности задача сводится к установлению функции распределения F ( х) некоторой случайной величины по данным независимым наблюдениям. К Асимптотические формулы в этом случае дают возможность оценить вероятную степень приближения, достигаемую при данном, не слишком малом объеме выборки, и обратно установить надлежащее число наблюдений так, чтобы с данной степенью вероятности гарантировать требуемую близость эмпирического распределения к теоретическому распределению вероятностей. [11]
Страницы: 1