Входное распределение

Cтраница 1

Входные распределения получают путем режимных наблюдений за содержанием того или иного изотопного индикатора во входных ( питающих) потоках. Входом многих ГГС являются атмосферные осадки, поэтому существует международная сеть станций Всемирной метеорологической организации ( МАГАТЭ), ведущих систематические наблюдения за содержанием Т, D и 18О, данные о которых регулярно публикуются. На территории СССР наблюдения ведутся по 18 станциям в европейской и по 19 станциям в азиатской частях страны. Поэтому для построения Свх ( f), как правило, приходится использовать прием достраивания рядов и их привязки к данным по станциям с наиболее продолжительным рядом наблюдений. [1]

Вследствие симметрии входного распределения и нечетности характеристики ограничителя очевидно, что математическое ожидание выходного процесса равно нулю. [2]

Указание: угадайте входное распределение и проверьте, что оно приводит к пропускной способности; это наиболее легкий путь получить здесь нужный результат. [3]

Указание: запишите входное распределение вероятностей в виде giQi ( K), где Qi ( k) является распределением вероятностей на входе г - го канала при условии, что используется i - й канал. [4]

К интерполяции промежуточных значений вероятности по ме - тоду наихудшего случая Оэ. [5]

V, в которых присутствует входное распределение помимо распределения погрешностей рабочего места. В этой связи в пакете необходимо присутствие подпрограммы идентификации ТО - в классе некоторых функций. [6]

Очевидно, для правильного понимания сетью входного распределения нужно, чтобы каждый элемент сети становился победителем одинаковое число раз - весовые векторы должны быть равновероятными. [7]

Выходом схемы ( также в зависимости от входного распределения Р ( х)) назначается выход одного из элементов инверсии. [8]

Входная и выходная плоскости здесь оптически сопряжены; входное распределение поля воспроизводится на выходной плоскости с изменением масштаба по двум координатам ( увеличением) в l / Dx Ах и в Ау раз ( напомним, что в силу (1.3) при Я О AD 1), соответствующим изменением интенсивности и добавлением некоего экспоненциального множителя с квадратично зависящим от х2, у2 показателем. В отсутствие амплитудных корректоров этот множитель является чисто фазовым; если на входе и выходе имеются гауссовы диафрагмы, то он описывает также уменьшение амплитуды за их счет. [9]

В этом выражении Н ( Y) зависит от входного распределения, а Н ( Z) не зависит. Таким образом, проблема нахождения пропускной способности для канала с аддитивным шумом сводится к максимизации Я ( У) при заданных ограничениях на входе. Следующие два примера показывают, как эта задача может быть иногда решена. [10]

Выразить пропускную способность через H ( Z) и найти входное распределение вероятностей, дающее максимум. [11]

Это Проявляется в том, что вне зависимости от характера входного распределения выходное тем больше приближается к нормальному, чем уже полоса Пропускания системы ширины спектра входного случайного процесса. [12]

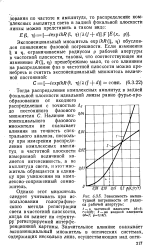Зависимость амплитудной погрешности от радиуса рабочей апертуры. [13]

Тогда распределение комплексных амплитуд в задней фокальной плоскости идеальной линзы равно фурье-пре-образованию от входного распределения с точностью Аа до постоянного фазового множителя С. [14]

Если начальное состояние не известно на передающем конце, то правильным будет так выбрать входное распределение, чтобы получить большую среднюю взаимную информацию для каждого возможного начального состояния. Нижняя пропускная способность С представляет собой наибольшую среднюю взаимную информацию на букву, которую можно достичь при фиксированном входном распределении, независимо от начального состояния. В этом примере можно показать, что С CN - 3 / 2 бит при любом N и что С достигается на статистически независимых и равновероятных входах. [15]

Страницы: 1 2