Оптимальное распределение - нагрузка
Cтраница 2
Задача оптимального распределения нагрузок между отдельными корпусами по выпаренной воде является одной из основных при автоматизации прямоточных многокорпусных выпарных установок ( МВУ) с промежуточным пароотбором. [16]
Задача оптимального распределения нагрузок между параллельно работающими абсорбционными аппаратами заключается в распределении газовой и жидкостной нагрузки и может быть поставлена в одном из следующих трех вариантов. [17]
Для оптимального распределения нагрузок между параллельными реакторами необходимо знать зависимость производительности реактора от нагрузки. [18]
При оптимальном распределении нагрузок на минимум себестоимости электроэнергии в энергообъединении исходя из цен на топливо и ядерное горючее относительные приросты стоимости расхода условного топлива на АЭС обычно ниже, чем на конденсационных электростанциях. В этом случае при Яаг 1 АЭС имеют обычно достаточно высокое использование в году. [19]
Поскольку критерием оптимального распределения нагрузок является получение минимума суммарных трудовых затрат, решение этой задачи сводится к определению минимума функции ряда независимых переменных от активных и реактивных мощностей. [20]
Исследуется проблема оптимального распределения нагрузок межцу параллельными технологическими линиями башенного отделения бромного производства. Установлено, что второй метод более предпочтителен, так как используются сравнительно простые вычислительные процедуры, и более удобен с точки зрения наглядности представления результатов. Приведены примеры расчета оптимальных распределений нагрузок для башенного отделения Перекопского бромного завода с подробным описанием процедуры поиска оптимума. [21]
Поэтому задачу оптимального распределения нагрузки между агрегатами выполняет вторичная система автоматического регулирования частоты и мощности. [22]
Для реализации оптимального распределения нагрузки с учетом потерь в сетях между ЧРЭС в процессе регулирования частоты и мощности по критерию (10.6) могут быть использованы и централизованный и децентрализованный методы. В дальнейшем в процессе разработки АСРЧ и М на их основе были синтезированы н другие методы н системы регулирования. [23]
Решение задачи оптимального распределения нагрузок в этом случае также решается путем приравнивания нулю. [24]
Рассмотрим задачу оптимального распределения нагрузок в сложной газотранспортной системе, исходя из минимума суммарных энергетических затрат при заданном объеме подачи газа и других планово-технологических ограничениях, как задачу математического программирования. [25]
Опишите условие оптимального распределения нагрузки между совместно работающими электростанциями без учета линий электропередачи. [26]
Поскольку критерием оптимального распределения нагрузок является получение минимума суммарных трудовых затрат, решение этой задачи сводится к определению минимума функции ряда независимых переменных от активных и реактивных мощностей. В ЭЭС число этих независимых переменных обусловлено различными конкретными условиями: балансом мощности, ограничениями по пропускной способности линий электропередачи и по вырабатываемой мощности отдельных электростанций и т.п. Дополнительно необходимо принимать во внимание еще и специфические особенности электроэнергетических установок: возможности повышения КПД парогенераторов, уменьшения потребления пара на собственные нужды турбин ТЭС и наивыгоднейшей установки лопаточного аппарата гидравлических турбин. [27]
Решение задачи оптимального распределения нагрузки рассмотрим на примере простейшего случая, когда число энергоблоков равно двум. [28]
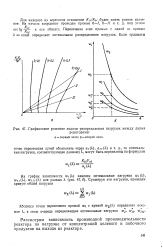 |
Графическое решение задачи распределения нагрузок между двумя. [29] |
К const определяет оптимальное распределение нагрузок. [30]
Страницы: 1 2 3 4