Оптимальное распределение - ресурс
Cтраница 1
Оптимальное распределение ресурсов является наиболее общей задачей исследования операций. При этом в одних случаях мы пытаемся достигнуть цели при минимальном расходе ресурсов ( средств) - ищем наиболее экономичные решения, а в других мы занимаемся поиском наиболее эффективных решений, позволяющих решить максимальное число задач, при использовании ограниченных ресурсов. Часто мы пытаемся решить комбинированную задачу, отыскивая такое оптимальное распределение ресурсов, которое обеспечивало бы наибольшую эффективность нашей управляющей деятельности. [1]
Оптимальное распределение ресурсов может быть получено кусочно-постоянным не более чем с N интервалами постоянства. [2]
Оптимальное распределение ресурсов с учетом их расширенного воспроизводства, структуры капитальных вложений - и срока ввода в действие строительных объектов дает решение динамической модели межотраслевого баланса. Однако чаще используют более простые модели матричного моделирования, распределения. [3]
Обеспечивает оптимальное распределение ресурсов на платформе PC, поддерживает все цвета без ограничения, сжатия не имеет. Многие программы трехмерного моделирования читают и записывают файлы в этом формате. [4]
Необходимо найти оптимальное распределение ресурсов на каждом этапе операции и общую эффективность. [5]
При этом оптимальное распределение ресурсов вдоль фиксированной трассы желательно совместить с задачей выбора трассы. Действительно, оптимальное решение каждой из этих проблем в отдельности ( выбор трассы, распределение вдоль нее имеющихся ресурсов) отнюдь не означает, что проблема в целом решена наилучшим образом. Полное значение критерия оптимальности при распределении ресурсов существенно зависит от того, вдоль какой трассы эти ресурсы распределяются. [6]
Рассмотрена задача оптимального распределения ресурсов по объектам, когда строительство ведется одной, двумя и более очередями. Процесс строительства рассматривается при этом как многошаговый процесс. С каждым шагом сопоставляется вектор выполнения работы и с первым связывается таблица распределения трудовых ресурсов, показывающая распределение ограниченных трудовых ресурсов по строящимся объектам для всех шагов. [7]
Рассмотрим задачу оптимального распределения ресурсов вдоль фиксированной трассы для двух важных для практики критериев, а затем покажем, лак может быть в этом случае решена задача выбора трассы. [8]
Если при оптимальном распределении ресурсов D вдоль некоторой трассы L параметр оптимизации Т принимает значение T L, то для любой части L0 трассы L при оптимальном распределении вдоль нее ( L0) тех же ресурсов D параметр оптимизации TLo s TL. Другими словами, при фиксированных ресурсах Z), которые предполагается распределить вдоль пути, параметр оптимизации является монотонно возрастающей функцией пути. [9]
В этом случае оптимальное распределение ресурсов сводится задаче выпуклого программирования. Ее численное решение в сколько-нибудь нетривиальных ситуациях обычно осложняется тем, что анализ каждого варианта распределения ресурсов требует сложного моделирования и соответственно большого объема вычислений. Поэтому к методу решения задачи (6.1) предъявляются жесткие требования по трудоемкости. [10]
Таким образом, оптимальное распределение ресурсов должно состоять из выпуклой комбинации капиталовложений в минимальные разрезы. [11]
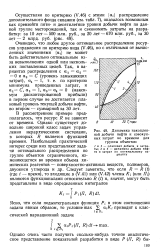 |
Динамика накопленной добычи нефти и совокупных затрат во времени для группы объектов. [12] |
Очевидно, что любое другое оптимальное распределение ресурсов управления по критерию вида (V.46), но с отличными от вычисленных значениями а ( - не может быть действительно оптимальным из-за невыполнения одной или нескольких поставленных целей. С, а2 1, а3 а4 0 ( максимум дисконтированной прибыли) в первом случае не достигается плановый уровень текущей добычи нефти, во втором - суммарной за 30 лет. [13]
Рассмотрим постановку задачи оптимального распределения ресурсов как основной составляющей модуля ресурсного обеспечения прогнозируемого облика объекта. [14]
Для сравнения были подсчитаны оптимальные распределения ресурсов для каждого варианта отдельно. [15]
Страницы: 1 2 3 4