Данное распределение
Cтраница 1
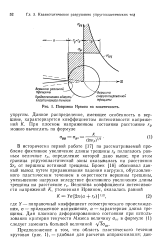 |
Поправка Ирвииа на пластичность. [1] |
Данное распределение, имеющее особенность в вершине, характеризуется коэффициентом интенсивности напряжений К. [2]
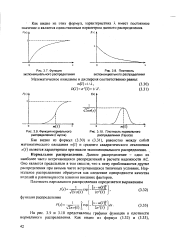 |
Функция [ IMAGE ] Плотность.| Функция нормального [ IMAGE ] Плотность нормального. [3] |
Данное распределение - одно из наиболее часто встречающихся распределений в расчете надежности АС. Оно является предельным в том смысле, что к нему приближаются другие распределения при весьма часто встречающихся типичных условиях. Нормальное распределение образуется как следствие однородности качества изделий и равномерности влияния внешних факторов. [4]
 |
Функция [ IMAGE ] Плотность. [5] |
Данное распределение встречается при анализе надежности АС и технических процессов с резервированием элементов, узлов АС или технологического оборудования. [6]
Данные распределения и граничные значения tq в зависимости от степени свободы и уровня значимости приведены в книгах по математической статистике. [7]
Данное распределение называется биномиальным, поскольку вероятности Рп, ь совпадают с членами разложения бинома Ньютона ( р q) n Биномиальное распределение - пример неравномерного распределения дискретной конечно-значной случайной величины. [8]
Данное распределение хорошо описывает различные совокупности проницаемости, кроме того, эта функция универсальная - она охватывает предельно широкий диапазон значений неоднородности - от нулевой до бесконечной большой. [9]
Данное распределение является усеченным гауссовским распределением величины n / по, если не считать того, что п - дискретная, а не непрерывная переменная. [10]
Данные распределения подтверждают практически полную диссоциацию хлористого лития в изоамиловом спирте. [11]
Данное распределение, ставящее в соответствие различным значениям х ( при известных N, p, q) вероятность их появления, называется биномиальным. [12]
Данное распределение также ступенчатое. [13]
Данное распределение называется распределением Стьюдента с п степенями свободы. [14]
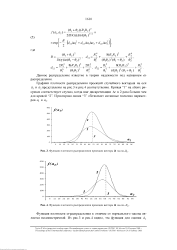 |
Функции плотности распределения проекции вектора Я.| Функции плотности распределения проекции вектора Я на ось Й2. [15] |
Страницы: 1 2 3 4