Полученное распределение

Cтраница 1

Полученное распределение имеет существенно меньшую дисперсию по сравнению с (2.1) при тех же значениях sc и зш. [1]

Полученное распределение называется распределением Ферми. При нуле температуры функция Ферми равна единице при е л и равна нулю при 6 IJL. Это означает, что в металлах л равно энергии Ферми Еф. Действительно, при Т 0 в имеющуюся электронную систему мы можем добавить электрон только с энергией Еф, так как все остальные состояния заняты. Вообще говоря, химпотенциал зависит от температуры. В изоляторах и полупроводниках, как мы увидим дальше, нет такой простой физической эквивалентности химпотенциала энергии Ферми. Из выражения для фермиевского распределения сразу следует, что при конечной температуре размытие верхней границы электронного спектра происходит, как мы и получили на основе качественных рассуждений, лишь в области порядка 2А БТ. [2]

Полученное распределение носит название распределения Шарлье. Для удобства пользования этим распределением в таблице XI Приложения протабулированы функция ф () и ее производные до четвертого порядка включительно. [3]

Полученное распределение носит название канонического распределения Гиббса. [4]

Полученные распределения по q ( S) еще не являются истинными. [5]

Полученное распределение потерь напряжения по фазам не превышает допустимого и может быть признано удовлетворительным. В практических расчетах следует пользоваться таблицами моментов, содержащимися в справочниках по светотехнике. [6]

Полученное распределение (3.18) носит название большого канонического распределения или распределения Гиббса. [7]

Полученные распределения при сделанных допущениях представляют собою полную информацию о влагосодержании дисперсного материала. [8]

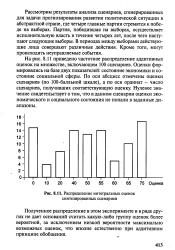Распределение интегральных оценок синтезированных сценариев. [9]

Полученное распределение в этом эксперименте и в ряде других не дает оснований считать какую-либо группу оценок более вероятной, за исключением низкой вероятности максимально возможных оценок, что вполне естественно при аддитивном принципе обобщения. [10]

Полученные распределения соответствуют тому, что каждый атом фосфора тетраэдрически окружен четырьмя атомами кислорода и каждый тетраэдр двумя вершинами связан с двумя соседними тетраэдрами. [11]

Результат расчетов - совокупность полей скоростей и давлений в поперечном сечении ДВК. [12]

Полученные распределения показывают численные значения скоростей и давления в каждой точке сечения ДВК. Получив серию подобных распределений, можно проследить зависимость этих значений от начальных и граничных условий. [13]

Получение случайных реализаций нескольких первичных параметров. [14]

Полученное распределение подвергают анализу, находят его оценки среднего значения и дисперсию. Если исследования конструкции производят с целью установления допусков, то по полученным оценкам устанавливают приемлемость выбранных допусков первичных параметров. [15]

Страницы: 1 2 3 4