Полученное распределение - температура
Cтраница 2
На рис. 222 показано распределение величин I TTJTJ) 4 и соответствующих температур t С в неподвижном плоскопараллельном слое поглощающей среды с оптической плотностью asl. Необходимо отметить, что полученное распределение температур отвечает лишь лучевому переносу тепла, без участия других видов переноса ( конвективного, турбулентного, молекулярного), а также при отсутствии источников тепла. Решение задачи лучевого переноса тепла с участием других видов переноса и источников тепла весьма усложняется и может быть выполнено лишь при упрощающих допущениях. [16]
При этом предполагается, что неосредненные значения температуры и концентрации описываются термодинамически равновесными соотношениями. На втором этапе по полученным распределениям температуры и концентраций находятся потери тепла излучением и учитывается их влияние на состав и температуру. На третьем этапе анализируется влияние кинетики химических реакций ( характеризующих выгорание топлива) на концентрацию реагирующих веществ и температуру пламени. [17]
В процессе решения запоминается распределение температуры по длине заготовок и сравнивается с первоначально заданным. Если расхождение превышает заданную погрешность, то происходит пересчет электрической задачи уже исходя из полученного распределения температуры и тепловой расчет повторяется. [18]
Если необходимо учитывать изменение мольных потоков пара и жидкости по высоте секций колонны, то в изложенный метод вносятся только небольшие изменения. Для обеспечения лучшей сходимости решения в этом случае целесообразно произвести расчет разделения сначала в предположении постоянства потоков пара и жидкости и использовать полученное распределение температур и концентраций в качестве первого приближения для расчета с изменением потоков. [19]
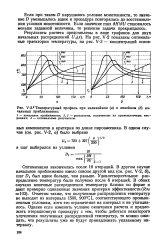 |
Температурный профиль при нелинейном ( а и линейном ( б начальных приближениях. [20] |
Удовлетворительное распределение температур было получено после 8 итераций. Отметим также, что полученные распределения температур не выходят из интервала [ 500, 900 С ], соответствующего промышленным условиям, хотя это ограничение на интервал и не учитывалось. [21]
В работе [1] исследуется влияние диссипации энергии на теплообмен при ламинарном течении неньютоновских жидкостей в круг-лнх трубах. Решение ищется методом Фурье в виде разложения в ряд по собственным функциям при постоянной температуре стенки. Достоверные данные получены при 9 собственных числах, дается количественная оценка влияния диссипации энергии. Имеющиеся в литературе решения других авторов получены для меньшего числа собственных чисел. Реализация решения [1] в практических целях требует большой вычислительной работы с привлечением ЭЦВМ. Кроме того, полученное распределение температуры экспериментально не проверялось. [22]
Страницы: 1 2