Последнее распределение

Cтраница 2

В литературе по надежности рассматриваются, например, такие законы распределения времени отказов: нормального распределения, распределения Релея, Гамма-распределения, распределения Вейбулла и др. Последнее распределение в известной мере является универсальным, охватывающим несколько других распределений. Например, закон экспоненциального распределения может рассматриваться как частный случай закона распределения Вейбулла. [16]

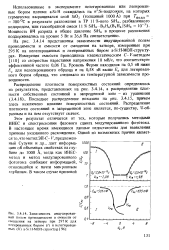Зависимость индуцированной полем проводимости и емкости от смещения на затворе при 297 К для легированных бором ( / и нелегированных ( / / а-51. Н - МОП-структур [ 96. [17]

Распределение плотности поверхностных состояний определялось из результатов, представленных на рис. 3.4.14, а распределение плотности собственных состояний в запрещенной зоне - из уравнения (3.4.18), Последнее распределение показано на рис. 3.4.15, причем здесь исключено влияние поверхностных состояний. Распределение плотности состояний в запрещенной зоне является, по-существу, U-об-разным и на нем отсутствует скачок. [18]

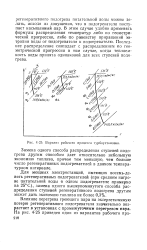Вариант рабочего процесса турбоустановки. [19]

В этом случае удобно применять формулы распределения температур либо по геометрической прогрессии, либо по равенству приращений энтропии воды от подогревателя к подогревателю. Последнее распределение совпадает с распределением по геометрической прогрессии в том случае, когда теплоемкость воды принята одинаковой для всех ступеней подогрева. [20]

В этом случае сопротивление обтеканию пузырьков жидкостью резко падает, так как жидкость, обтекая пузырек, поступает в соседние трубки тока. Вследствие того, что любая система стремится к минимуму диссипации энергии, последнее распределение пузырьков в потоке будет предпочтительнее. Естественно, это распределение не будет идеально кубическим или ромбоэдрическим из-за некоторого различия в размерах пузырьков и, следовательно, в скорости их относительного движения в жидкости, но тем не менее оно будет близко к таковому. Таким образом, в так называемом стесненном потоке, при всплытии больших групп пузырьков или в течении смеси при пузырьковой или эмульсионной структурах относительная скорость движения больше, чем у одиночных пузырьков такого же размера. [21]

При алкилировавии толуола метилхлоридом ч хлоридом алюминия н обработки реакционной смеси водой через 1 мин после начала реакции распределение ксилолов было следующим: 55 % о -, 10 % м - и 35 % гг-изомера. Если реакция протекала в течение нескольких часов, то после обработки водой распределение продуктов было следующим: 20 % о -, 60 % м - и 20 % re - ксилола. Последнее распределение наблюдается и в том случаи, если любой из изомерных ксилолов оставить на некоторое время в контакте с безводным хлористым водородом и следовым количеством хлорида алюминия. [22]

В приведенной таблице поражает удивительно малый разброс эффективности восстановления для столь различных распределений длительности восстановления, которые были нами выбраны. Несколько большая эффективность, которая имеет место для первых двух распределений. То, что последнее распределение требует одного и того же времени для любого восстановления. Близость цифр, приведенных в таблице, является следствием следующей теоремы. [23]

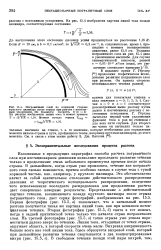Пограничный слой на кормовой стороне круглого цилиндра после отрыва при разгоне с постоянным ускорением. По Блазиусу. Скорость 17 ( 0 Ы На рисунке изображены линии тока в момент времени. [24]

Изложенные в предыдущих параграфах способы расчета пограничного слоя при нестационарном движении позволяют проследить развитие течения только в продолжение очень небольшого промежутка времени после начала отрыва. В дальнейшем, когда отрыв уже произошел, течение вне пограничного слоя сильно изменяется, причем особенно сильно в случае тела с тупой кормовой частью, как, например, у круглого цилиндра. Это обстоятельство влечет за собой значительное отклонение действительного распределения давления от теоретического потенциального распределения, вследствие чего использование последнего распределения для продолжения расчета дает совершенно неверные результаты. Представление о действительной картине течения, возникающего позади круглого цилиндра после отрыва пограничного слоя, дает серия фотографий, изображенных на рис. 15.5. Первая фотографии ( рис. 15.5, а) показывает, что в начальный момент разгона получается такая же картина линий тока, как при невязком потенциальном течении. Вторая фотография ( рис. 15.5, б) снята в тот момент, когда в задней критической точке только что начался отрыв пограничного слоя. На третьей фотографии ( рис. 15.5, в) точка отрыва уже успела переместиться далеко вверх по течению. Линия тока, отходящая от точки отрыва, окружает область, в которой скорости очень малы. [25]

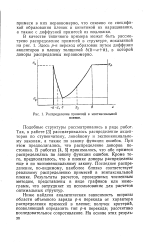Распределение примесей в эпитаксиалыюй пленке. [26]

Кроме того, предполагалось, что в пленке доноры распределены еще и по экспоненциальному закону. Последнее распределение, по-видимому, наиболее близко соответствует реальному распределению примесей в эпитаксиальной пленке. Результаты расчетов, проведенных численным методом, представлены в виде графиков или номограмм, что затрудняет их использование для расчетов оптимальных структур. [27]

Страницы: 1 2