Простое распределение

Cтраница 3

Более точные аппроксимации биномиального закона, упоминавшиеся выше, имеют то преимущество, что они более точны, и тот недостаток, что они более сложны. В то же время простое распределение Пуассона обладает сравнительно универсальной применимостью. Последнее утверждение мы понимаем в том смысле, что если экспериментальные данные показывают, что закон Пуассона неприменим, в то время как, сообразно со здравым смыслом, он должен был бы действовать, то естественнее подвергнуть сомнению статистическую устойчивость наших данных, чем искать какой-то другой закон распределения. Следовательно, почти тривиальное, с математической точки зрения, доказательство теоремы 4.5 нужно рассматривать как эвристический прием, приводящий нас к одному из универсальных ( в рамках применимости теории вероятностей) законов природы. [31]

Вероятностные распределения с операцией свертки образуют алгебраическую структуру, содержащую множество неразложимых распределений ( например, каждое распределение, сосредоточенное в двух точках, неразложимо), но в ней нет ни одного простого распределения. Следовательно, если мы действительно считаем простые распределения атомами, то здесь вообще нет атомов. [32]

Некоторые расчеты характеристик турбулентных течений при естественной конвекции около вертикальной поверхности выполнены в работах [17, 107, 117] с использованием моделей турбулентности первого порядка. Как и при исследовании вынужденной конвекции, задавались простые распределения турбулентной вязкости, В работах [116, 124] Для расчета турбулентной вязкости с помощью уравнений для соответствующих параметров турбулентности ( / С, е) применена ( К - е) - модель. В последней работе использовался метод Джонса и Лаундера [78], предложенный для течений, развивающихся в условиях вынужденной конвекции. Масштабом длины служил масштаб длины диссипации. [33]

В этом случае предполагается известной только суммарная средняя интенсивность исполнения всей совокупности функционирующих групп программ без классификации их по каким-либо признакам. Интегральное распределение длительностей обслуживания при этом приходится аппроксимировать достаточно простым распределением. Наиболее удобным распределением является экспоненциальное, которое достаточно хорошо подтверждается экспериментальными исследованиями реальных длительностей решения больших совокупностей задач при отсутствии селекции потоков. [34]

Деформация и яркостная пульсация части поля в телекинопроекторе могут иметь весьма различные сложные распределения по площади изображения, зависящие от системы и конструктивного решения отдельных элементов установки. Для упрощения проведения экспертиз было решено ограничиться одним относительно простым распределением яр косгных пульсаций по экспоненциальному закону для вертикального направления с максимумом в верхней части изображения и с постоянной величиной по горизонтальному направлению. [35]

Примеры, приведенные в разделе 2.6, включали использование простого распределения вероятностей, основанного на оценке предыдущих значений. [36]

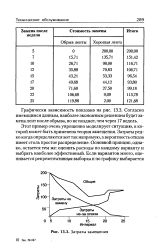Затраты замещения. [37]

Этот пример очень упрощенно моделирует ситуацию, в которой может быть применена теория замещения. Затраты редко когда определяются вот так напрямую, а вероятность отказа имеет столь простое распределение. Основной принцип, однако, остается тем же: оценить расходы по каждому варианту и выбрать наиболее эффективный. [38]

Одну из разновидностей сверхзвуковой схемы представляет собой крыло треугольной формы в плане, иногда называемое дельта-крыло. Эта форма в плане имеет значительный теоретический интерес, так как для дельта-крыльев с некоторыми простыми распределениями угла атаки прямая задача теории крыла может быть решена сравнительно легко. В предыдущих разделах были изложены два общих метода вычисления потока, создаваемого тонкими телами и крыльями: метод источников и метод интеграла Фурье. [39]

Заметим, что при случайном спросе на продукт, хранящийся на складе, мы уже не знаем заранее, какое количество продукта будет потребовано за период между моментом заказа и моментом поставки заказанного продукта, что, вообще говоря, приводит к необходимости держать на складе больший запас, чем при детерминированном спросе. Решение задачи о выборе оптимальных значений величин s и q удается провести аналитическим путем только в случае достаточно простых распределений случайных величин, используемых в модели исследуемой системы хранения запаса. Если же распределения сложны, параметры распределений меняются со временем или исследуемая система состоит из нескольких связанных между собой складов, в которых одновременно хранятся, быть может, продукты разного типа, то единственным средством исследования такой системы пока остаются имитационные эксперименты, которым посвящена последняя глава нашей книги. Заметим что в задачах массового обслуживания и управления запасами имитационное исследование проблемы часто называется методом Монте-Карло. [40]

Особенно рельефно топологические факторы проявляются при гетерогенной и гетерофазной полимеризации. Они тоже могут быть учтены в обобщенной функции вида (1.2), которая скорее всего будет представлять собой комбинацию простых распределений, каждое из которых соответствует некоторому частному механизму полимеризации. [41]

Страницы: 1 2 3