Экспериментальное распределение - давление
Cтраница 1
Экспериментальное распределение давлений по внутренней поверхности колеса определяется значительно сложнее, чем по наружной. [1]
Экспериментальное распределение давлений для конфузорнон решетки с осевым входом ( соплового аппарата) дает удовлетворительное совпадение с теоретической кривой потенциального обтекания1) ( фиг. [2]
Приведенные ниже значения величины ksv / v получены из экспериментального распределения давления путем рассуждений, о которых будет сказано ниже. Указанные числа относятся только к песочной шероховатости. [4]
В этом случае, как упоминалось, необходимо учитывать обратное влияние пограничного слоя на потенциальное обтекание или пользоваться экспериментальным распределением давления по поверхности профиля. [5]
Цель работы - ознакомление с расчетом установившихся одномерных течений идеального газа, экспериментальное исследование течений газа в коническом сверхзвуковом сопле и сравнение экспериментального распределения давления с рассчитанным теоретически. [6]
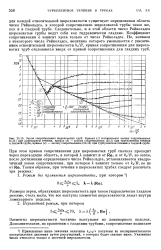
Действительно, если при этом применять уравнения Прандтля до точки отрыва, то распределение давления в слое уже нельзя брать из плавного потенциального обтекания, так как отрыв резко его искажает. В этом случае, как упоминалось, необходимо учитывать обратное влияние пограничного слоя на потенциальное обтекание или пользоваться экспериментальным распределением давления по поверхности профиля. Для подтверждения этого факта достаточно обратиться к рис. 58 и 59 ( стр. Отчетливо видна разница между распределением коэффициента давления по поверхности круглого цилиндра, рассчитанными по теоретическому безвихревому обтеканию идеальной несжимаемой жидкостью ( на рис. 58 - теор. [7]
 |
Функции / i и / з ряда Блазиу-са ( таблицы и. [8] |
Применим изложенный способ расчета пограничного слоя к обтеканию круглого цилиндра, причем для получения однозначных соотношений возьмем в качестве основы для расчета теоретическое потенциальное распределение давления, хотя в литературе за такую основу обычно берется экспериментальное распределение давления. Пусть потенциальное течение набегает на круглый цилиндр радиуса R со скоростью [ /, направленной параллельно оси х, и пусть обтекание цилиндра происходит без циркуляции. [9]
 |
Сравнение параметров пограничного слоя. [10] |
Польгаузен использовал экспериментальное распределение давления на поверхности круглого цилиндра, полученное К. [11]
При наличии отрыва пограничного слоя обтекание тела перестает быть плавным. Область пограничного слоя, включая сюда сорвавшийся слой и аэродинамический след, несмотря на большие значения рейнольдсова числа, уже не тонка, и изложенная теория теряет силу. Действительно, если при этом применять уравнения Прандтля до точки отрыва, то распределение давления в слое уже нельзя брать из плавного потенциального обтекания, так как отрыв его резко искажает. В этом случае необходимо принимать во внимание обратное влияние пограничного слоя на потенциальное обтекание или, что проще, пользоваться экспериментальным распределением давления по поверхности профиля. Для подтверждения этого факта достаточно обратиться к рис. 58 и 59 ( стр. Отчетливо видна разница между распределением коэффициента давления по поверхности круглого цилиндра, рассчитанными по теоретическому безвихревому обтеканию идеальной несжимаемой жидкостью ( на рис. 58 - теор. [12]
Процесс взаимодействия УВ со слоем насыпной плотности, лежащим на дне вертикальной ударной трубы, моделируется с помощью точечной математической модели. Она основана на предположении о том, что участок слоя пыли можно заменить некоторым объемом, обладающим точечной массой. Эта масса находится под действием кулонова трения и упругой силы с постоянным коэффициентом упругости. При этих предположениях модель представляется в виде обыкновенного дифференциального уравнения второго порядка, для которого поставлена задача Коши. Входные параметры модели ( коэффициенты кулонова трения, упругости и др.) определяются из экспериментального распределения давления во времени для слоя толщиной 14 мм. [13]
Страницы: 1