Кривое распределение - частица
Cтраница 2
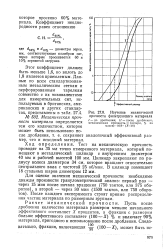
Во всех трех случаях расчетные кривые распределения частиц по размерам обладают асимметричной формой, круто обрываясь на стороне больших размеров и имея длинный хвост в сторону малых диаметров. Ширина распределений наибольшая для первого процесса и наименьшая для третьего процесса. В последнем случае, по-видимому, происходила коалесценция кластеров в результате их столкновений при броуновском движении, хотя механизм миграции кластеров недостаточно ясен. Вообще говоря, существующие теории только качественно описывают наиболее характерные особенности роста частиц в матрице, тогда как количественное согласие теоретических предсказаний с экспериментальными данными отсутствует. [16]
 |
Изучение механической прочности фильтрующего материала. [17] |
После каждого эксперимента строят кривые распределения частиц материала по размерным группам. [18]
Ввиду того, что экспериментальные численные кривые распределения частиц по размерам при обезвоживании растворов в кипящем слое практически во многих случаях имеют очень сложный бимодальный характер [ 8; 9, с. В результате дробления крупных гранул ( минусовый источник в области крупных частиц) образуются мелкие частицы, распределение по размерам которых имеет бимодальный характер. Наличие бимодальности распределения новых центров грануляции указывает на то, что при дроблении образуются частицы двух классов крупности. [19]
Как строят дифференциальную и интегральную кривые распределения частиц материала по размерам. [20]
Такой механизм объясняет бимодальный характер кривых распределения частиц слоя по размерам. [21]
Какую информацию о дисперсной системе дают интегральная и дифференциальная кривые распределения частиц по размерам. [22]
 |
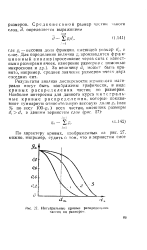
Дифферента тьная крипяя рас-пределенил частиц полидиеперснои системы по радиусам. [23] |
Результаты дисперсионного анализа полидисперсных систем представляют также в виде кривых распределения частиц по размерам, характеризующих степень полидисперсности системы. [24]
Проведена оценка дисперсности порошков силикагелей разных фракций с помощью кривых распределения частиц по размерам и определена оптимальная фракция, отвечающая мономодальному распределению. [25]
Такое рассмотрение процесса позволяет легко найти общее частиц и построить кривые распределения частиц по раз-мерам для любой степени разложения исходного ацетилена. Сле-повательно, при помощи такого расчета можно построить кривые, выражающие зависимость числа образовавшихся частиц и тол-образовавшегося слоя углерода от степени разложения ацетилена. [26]
Более строгая характеристика дисперсности аэрозолей может быть получена на основе кривых распределения частиц по размерам ( гл. [27]
Результаты седиментационного анализа дисперсности полидисперсных систем представляют также в виде кривых распределения частиц по размерам, характеризующих степень полидисперсности системы. [28]
Более строгая характеристика дисперсности аэрозолей может быть получена на основе кривых распределения частиц по размерам ( гл. [29]
 |
Интегральные кривые распределения частиц по размерам. [30] |
Страницы: 1 2 3 4 5