Рассеяние - результат
Cтраница 3
Параметр s, являющийся мерой рассеяния результатов испытания по каждой партии катализатора, отражает степень ее однородности. Заметим, что ни / ср, ни s в отдельности не являются исчерпывающими характеристиками, и лишь их совокупность дает достаточную информацию о прочностных свойствах всей партии в целом. [31]
Однако последний зависит не только от рассеяния результатов, но и от расстояния между наибольшим и наименьшим результатами. Поэтому коэффициент корреляции не следует рассматривать как подходящий показатель для проверки линейности. [32]
 |
Графики плотности распределения вероятности отсчета при различной дисперсии. [33] |
Чем больше дисперсия, тем значительнее рассеяние результатов, полученных по формулам ( 2), ( 7) относительно хТ Это наглядно видно на рис. 16, где представлены кривые плотности одного и того же закона распределения вероятности отсчета при различных дисперсиях. [34]
 |
Графики плотности распределения вероятности отсчета при различной дисперсии. [35] |
Чем больше дисперсия, тем значительнее рассеяние результатов, полученных по формулам ( 2), ( 7) относительно Z Это наглядно видно на рис. 16, где представлены кривые плотности одного и того же закона распределения вероятности отсчета при различных дисперсиях. [36]
Статистическая природа процесса усталостного разрушения предопределяет рассеяние результатов испытаний на усталость. [37]
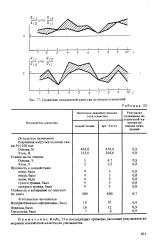 |
Сравнение показателей качества по шкале отношений. [38] |
В табл. 23 и последующих примерах рассеяние результатов измерения показателей качества не учитывается. [39]
Это второе допущение означает, что случайные рассеяния результатов наблюдений вокруг измеряемой величины не могут безгранично возрастать. [40]
Остаточная сумма, наоборот, учитывает рассеяние результатов внутри отдельных групп около группового среднего х /, Гр при закрепленном уровне фактора FJ. Таким образом, остаточная сумма отражает влияние случайных помех на результат анализа. [41]
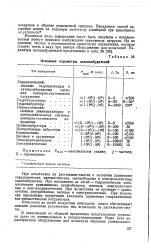 |
Основные параметры силовозбудителей. [42] |
Испытания на изгиб вследствие небольших помех обеспечивают меньшее рассеяние результатов, чем испытания на растяжение-сжатие. [43]
Закон распределения результатов наблюдений позволяет количественно оценить рассеяние результатов наблюдений и средних (1.1) около Хг. Существуют границы Xr k ( Xy, в которых лежит основная часть ( Р %) выборочных средних. Интервал значений средних Хг - г - f - A и вероятность Р называются доверительными. [44]
Получены математические выражения для ошибки, характеризующей рассеяние результатов анализа при работе по методу добавок. [45]
Страницы: 1 2 3 4