Изотропное рассеяние

Cтраница 2

Преобразуем уравнение аналогично случаю изотропного рассеяния частиц. [16]

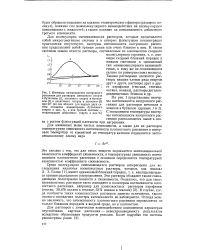
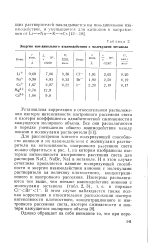
Время релаксации анизотропии в индивидуальных жидкостях и растворах.| Изотермы интенсивности рассеяния для тройных растворов бутиловый спирт - ацетон - этиловый спирт при 20. [17]

Верхние кривые относятся к изотропному рассеянию, а нижние - к анизотропному. [18]

Таким образом, при изотропном рассеянии частицы полностью теряют импульс в первоначальном направлении в среднем за одно столкновение. [19]

Изотермы интенсивности изотропного рассеяния для растворов метилового спирта в бутиловом ( 1, этилового спирта в бутиловом ( 2 и децилового спирта в этиловом ( 3 при 20 ( по оси абсцисс для первых двух систем отложена концентрация бутилового спирта в мол. %, а для третьей системы - концентрация децилового спирта в мол. %. [20]

С повышением температуры изотермы интенсивности изотропного рассеяния располагаются выше в связи с ростом флюктуации плотности при нагревании. [21]

Таким образом, эта модель дает изотропное рассеяние частиц. [22]

Изотермы интенсивности изотропного рассеяния для системы масляная кислота - вода при различных температурах ( по оси абсцисс отложена концентрация масляной кислоты в вес. %.| Зависимость интенсивности изотропного рассеяния от превышения температуры над критической Д для 24 4 % - ного ( 1, 49 1 % - ного ( 2 и 74 3 % - ного ( 3 растворов масляной кислоты в воде. [23]

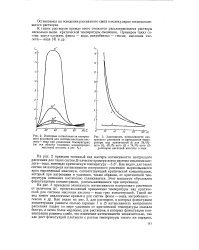
На рис. 3 приведена зависимость интенсивности изотропного рассеяния от величины А. [24]

На рис. 6 представлены политермы интенсивности изотропного рассеяния света для системы нафталин - ментол различных концентраций. Для остальных систем политермы имеют качественно сходный вид. На многих из них наблюдаются минимумы при температурах, относительно близких к температурам плавления, или участки, где интенсивность практически не изменяется с температурой. На политермах для эвтектических концентраций эти минимумы выражены сильнее. [25]

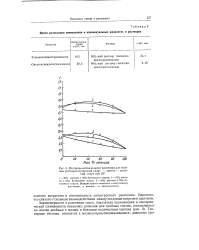
Изотермы интснсивпо -. ти изотропного и анизотропною рассеяния света в растворах LiCl в - спиртах при Т. [26]

На рис. 3 приведены изотермы интенсивности изотропного рассеяния света для указанных растворов. [27]

Таким образом, минимум на изотермах интенсивности изотропного рассеяния обусловлен изменением интенсивности плотностного и концентрационного рассеяния с ростом концентрации электролита в противоположных направлениях. [28]

Простейшим из возможных вариантов рассеяния является случай изотропного рассеяния, характеризующийся тем, что все направления движения электрона после столкновения равновероятны. В этом случае скорость дрейфа, приобретенная электроном под действием поля в течение свободного пути пробега, полностью теряется в процессе столкновения. Как будет видно из дальнейшего ( см. § 4), такое положение имеет место в случае рассеяния на тепловых колебаниях решетки. При других механизмах рассеяния ( в частности, для рассеяния кулоновским полем ионизированных примесных центров) преобладает рассеяние под малыми углами. В этом случае интегральное сечение рассеяния 0 (, определяемое равенством (5.2), удобнее заменить другим интегральным сечением рассеяния 0С, которое получается в результате усреднения 0 ( 0, ф) надлежащей весовой функцией, учитывающей изменение скорости дрейфа при соударении. [29]

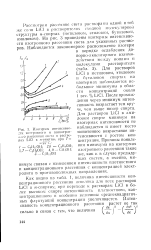
Энергия ион-дипольного взаимодействия с молекулами метанола. [30]

Страницы: 1 2 3 4 5