Максимальная величина - отклонение
Cтраница 1
 |
График импульсного воздействия ультразвуковых колебаний. [1] |
Максимальная величина отклонения w платы ( если иГ / 2) достигается после окончания действия силы. [2]
Предварительно приняв максимальную величину отклонения ординат точек ломаной линии от ординат точек исходной кривой ( при одной и той же величине абсциссы), можно построить такую ломаную линию. Естественно, при выборе указанной величины отклонения ординат точек ( отрезки / - 1, 2 - У и 3 - 5) следует учитывать степень точности построения кривой зависимости k ( ли а) от состава сырья. [3]
В табл. 6 приводятся отношения максимальных величин отклонений от аддитивности плотности и атомной концентрации. [4]
В качестве критериев принимаются: SE, макс - максимальная величина отклонения точки Е от вертикали, определяемая габаритами ОТ ( кинематический критерий); 712, 2з - допускаемые углы давления в кинематических парах В и С ( динамический критерий); BD LC - расстояние, определяющее габариты механизма захвата. [5]
Современные представления о необходимой степени равномерности потока в рабочей части сверхзвуковой аэродинамической трубы определяют максимальную величину отклонений числа Маха от среднего значения в долях процента. Важным фактором, характеризующим качество потока, является также спектральная характеристика неравномерности: ясно, что в соплах аэродинамических труб наиболее нежелательны возмущения с длиной волны порядка характерного размера модели. Эти условия и определяют высокие требования к точности расчетов: она должна превосходить возможности металлообработки. Следует заметить, что в настоящее время в большинстве трубных сопел неравномерность потока по числу М не меньше Ь ( 1 - 2) %, а точность расчетов Ь ( 1 - 3) % в задачах внешней аэродинамики все еще считается удовлетворительной. Таким образом, точность расчета сопел должна значительно превышать точность расчета других задач аэродинамики и находится, фактически, на грани возможностей современной вычислительной техники. При этом весьма важно также знать, в каких местах расчетной области происходит концентрация вычислительной погрешности. Таким местом, несомненно, является область трансзвуковых скоростей, поэтому точность профилирования должна быть выше всего именно в окрестности критического сечения сопла. [6]
В нормальных условиях, когда нет резких и больших колебаний нагрузки, качество регулирования может быть оценено по максимальной величине отклонения регулируемою параметра от заданного значения. В некоторых случаях это отклонение настолько велико, что применение регулятора данного типа делается невозможным. [7]
Случайные отклонения параметров могут иметь разные знаки, поэтому при рарчете их необходимо складывать, чтобы получить и оценить максимальную величину отклонения исследуемого параметра. [8]
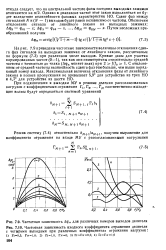
На рис. 7.9 приведены частотные зависимости величины отклонения сдвига фаз сигналов на выходных зажимах от линейного закона, рассчитанные по формуле (7.3) при различном числе выходов. Максимальная величина отклонения фазы от линейного закона в полосе пропускания не превышает 5 9 для устройства из трех НО и 4 7 для устройства из шести НО. [10]
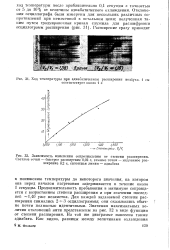
Продолжительность пребывания в минимуме сокращается с возрастанием степени расширения и при значении последней - 1 40 уже незаметна. Для каждой задаваемой степени расширения снимались 2 - г - 3 осциллограммы; они оказывались обычно почти полностью идентичными. Значения максимальных величин отклонений нити представлены на рис. 32 в виде функции от степени расширения. На той же диаграмме нанесена также адиабата. [12]
Существуют два пути решения вопроса о закономерностях, которым подчиняется изотерма данного свойства в системе с химически невзаимодействующими компонентами. Первый из них приложим к группе свойств, для которых проведен обоснованный вывод изотермы идеальной системы. Тогда, рассчитывая отклонения от идеальности достаточно большого числа систем, можно установить максимальные величины отклонений, которые вызываются нехимическими взаимодействиями, а также связать эти отклонения со свойствами компонентов. Зная эти характеристики, можно из анализа диаграммы реальной системы установить, протекает ли в системе взаимодействие. Очевидно, что суждение это будет обоснованным лишь в том случае, если отклонения экспериментальной изотермы от идеальной превысят отклонения, которые могут быть вызваны нехимическими взаимодействиями. [13]
Одним из основных этапов конструирования пластмассовой детали является выбор рациональных допусков на размеры. Эту задачу можно решить, если известна достижимая точность изготовления деталей из пластмасс. Вопросы технологии изготовления пластмассовых изделий подробно рассмотрены в следующей главе. Здесь в качестве примера приведена номограмма Р. М. Кругликова и др. ( рис. 24), по которой можно определить: а) точность изготовления деталей из пластмасс, максимальную величину отклонения номинальных размеров ДХР. [14]
Страницы: 1