Знак - член
Cтраница 1
Знаки членов второй суммы, а они могут быть как положительными, так и отрицательными, целесообразно идентифицировать со знаками количеств облучения, считая безразмерные избыточные температуры и остальные сомножители положительными. [1]
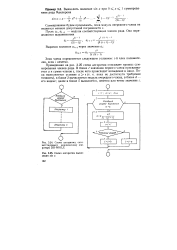 |
Схема алгоритма, соответствующего циклическому оператору DO-WHILE.| Схема алгоритма вычисления sin х. [2] |
Знак члена определяется следующим условием: г - й член положителен, если t нечетно. [3]
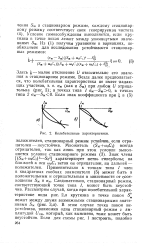 |
Колебательные характеристики. [4] |
Знак члена [ ( SM o) oCi) 2 - 5б2 ] характеризует ветвь гиперболы; на ближней к оси tioCi ветви он отрицателен, на дальней - положителен. Применительно к точкам типа 1 член в квадратных скобках знаменателя ( 5) может быть и положительным и отрицательным в зависимости от соотношения SM и стм. Следовательно, стационарный режим, соответствующий точке типа /, может быть неустойчив. В этом случае точка покоя неустойчива, возможен один стационарный режим с амплитудой U cm, который, ак выяснено, тоже может быть неустойчив. [5]
 |
Разделение бензола на две части, R и S. [6] |
Знак членов bos выбирается с таким расчетом, чтобы величина AWrt была положительной. [7]
Знаки членов р, - Zj и pi - ph определяются порядком чередования действительных, отрицательных и простых полюсов и нулей. [8]
Знаки членов чередуются; правые части обрываются сами собой, заканчиваясь нулевой или Первой степенью косинуса. [9]
Знак члена совпадает со знаком ( - 1), где t - число инверсий в перестановке вторых индексов элементов члена при условии, что первые индексы расположены в порядке возрастания. [10]
Знаки членов формулы Д, устанавливаются по следующему правилу. Если характеры температурной деформации и деформации, вызываемой единичной нагрузкой, совпадают, то знак соответствующего члена будет положительным, и наоборот. [11]
Знаки членов первой суммы целесообразно идентифицировать со знаками характерных начальных избыточных температур, считая приведенные безразмерные избыточные температуры положительными. [12]
Когда знаки членов ряда чередуются, то их взаимное уничтожение может затруднить получение асимптотической оценки. Обычно лучше иметь дело с соответствующей производящей функцией, если она существует. Простым источником знакочере-дования в комбинаторике является принцип включения-исключения, который вкратце будет разобран. В этом случае часто бывает невозможно найти производящую функцию, поэтому важно иметь метод, непосредственно оперирующий с суммой. Технический прием, описываемый здесь, будет работать только тогда, когда в сумме доминируют начальные члены. [13]
Если знаки членов ряда сп выбирать произвольно, то вероятность сходимости или расходимости этого ряда равна 1, смотря по тому, сходится ряд с или расходится. [14]
Для определения знака члена определителя не обязательно располагать элементы члена в порядке возрастания первых индексов. Об этом говорит следующая теорема. [15]
Страницы: 1 2 3 4