Рассмотрение - дифракция
Cтраница 3
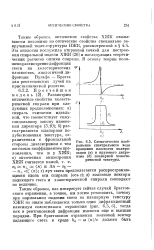 |
Схематическое изображение спектрального хода вращения плоскости поляризации ( а и кругового дихроизма ( б планарной холестерической текстуры. [31] |
Таким образом, оптические свойства ХЖК оказываются похожими на оптические свойства специально закрученной твист-структуры НЖК, рассмотренной в § 4.4. Эта аналогия послужила отправной точкой для построения спиральной модели ХЖК [26] и последующих теоретических расчетов оптики спирали. В основу теории положено рассмотрение дифракции света на холестерических плоскостях, аналогичной дифракции Вульфа - Брэгга для рентгеновских лучей на кристаллической решетке. [32]
Как мы видели при рассмотрении дифракции света от круглого отверстия ( когда площади зон Френеля были равными), сложение амплитуд дает кривую в виде спирали. [33]
Практические ограничения, которые обсуждались при рассмотрении просвечивающей дифракции, справедливы и в этом случае, так как и здесь необходимо или отделить пленку от ее подложки, или сделать подложку тоньше после нанесения пленки, или использовать очень тонкие подложки, которые прозрачны для электронов, например, угольные пленки или чешуйки слюды. Ход лучей в просвечивающем мироскопе показан на рис. 6 а. В большинстве электронных микроскопов используют магнитные линзы. Образцы освещаются посредством сдвоенной конденсорной системы, которая позволяет выбирать расходимость падающего пучка и размеры облучаемой площадки образцу. Обычно эти размеры колеблются в пределах 2 - 20 мкм. Пучок после прд-хождения через образец попадает в линзу объектива, которая имеет возможность корректировать астигматизм. [34]
Вероятностный характер такой системы легко продемонстрировать на примере рассмотрения дифракции светового луча при прохождении узкой щели. Если за щелью поместить фотографическую пластинку, то после необходимой экспозиции получается дифракционная картина, на которой будут видны темные и светлые области, соответствующие высокой и низкой интенсивности. Если рассмотреть луч с очень малой интенсивностью, то очевидно, что мы не сможем точно указать, в какое место пластинки попадают фотоны. [35]
Дополненный впоследствии применением преобразования Фурье к формированию изображения объектов с непериодической структурой, подход Аббе проявился в создании многих исключительно важных методов. Как уже упоминалось, они зависят главным образом от рассмотрения фраунгоферовой дифракции с точки зрения пространственных частот и доступности дифракционной картины как математически, так и экспериментально в случае использования когерентных условий. [36]
Характер рассматриваемой структуры определяет значения амплитуд и фаз отдельных синусоидальных членов ряда. Таким образом, дифракцию на сложной структуре можно рассчитать путем рассмотрения дифракции на каждой отдельной компоненте разложения Фурье этой структуры. Так как периоды синусоидальных структур различны, то и углы дифракции соответствующих максимумов первого порядка будут различны, и в совокупности получится полная дифракционная картина всей структуры. [37]
Характер рассматриваемой структуры определяет значения амплитуд и фаз отдельных синусоидальных членов ряда. Таким образом, дифракцию на сложной структуре можно рассчитать путем рассмотрения дифракции на каждой отдельной компоненте разложения Фурье этой структуры. Так как периоды синусоидальных структур различны, то и углы дифракции соответствующих максимумов первого порядка будут различны, и в совокупности получится полная дифракционная картина всей структуры. С этой точки зрения максимумы высших порядков обычной дифракционной решетки суть максимумы первого порядка соответствующей ей синусоидальной слагающей. Таким образом, для изученной нами одномерной решетки ( решетка с коэффициентом пропускания, меняющимся только вдоль одной координаты) мы с помощью этого более общего способа рассмотрения получаем согласный с опытом результат. [38]
Эта проблема ( составляющая предмет теории дифракции) очень важна для оптики и теории распространения радиоволн. Из курса общей физики читатель знаком с элементарной формулировкой принципа Гюйгенса и методом рассмотрения дифракции с помощью зон Френеля. [39]
Представление об обратной решетке возникло непосредственно из задачи разложения в ряд Фурье функции, обладающей периодичностью прямой решетки. В дальнейшем мы увидим, как понятие об обратной решетке плодотворно используется при рассмотрении дифракции рентгеновских лучей в кристаллах, при исследовании колебаний атомов в кристаллах и при квантовомеханическом изучении движения электрона в периодическом поле. [40]
Представление о волноводной дифракции имеет широкое значение и используется не только при описании изолированных структур. Матрица S, а также матрицы Z и У могут быть применены и при рассмотрении дифракции в свободном пространстве. [41]
Объемные дефекты удовлетворительно выявляются совмещенным преобразователем независимо от направления падающей волны. Помимо непосредственно отраженного эхосигнала от объемного дефекта с гладкой поверхностью наблюдают сигналы от волны, обежавшей вокруг дефекта, как было отмечено при рассмотрении дифракции на цилиндре. [42]
В частности, препятствия с мнимыми поверхностными импеданса-ми возбуждают поверхностные волны. Для хорошего металлического проводника 0В тг / 2 - i / k, так что на его поверхности может распространяться поверхностная волна, которая проникает на некоторую конечную глубину в металл. При рассмотрении дифракции на клиньях, отверстиях и других объектах с поверхностным импедансом необходимо учитывать, что поверхностные волны могут вносить изменения как в интенсивность, так и в фазу суммарного дифрагированного поля. [43]
Это уравнение показывает, что имеется определенная связь между плотностью частиц и квадратом волновой функции. Вероятностный характер такой системы легко продемонстрировать на примере рассмотрения дифракции светового луча при прохождении узкой щели. Если за щелью поместить фотографическую пластинку, то после соответствующей экспозиции получается дифракционная картина, на которой будут видны темные и светлые области, соответствующие высокой и низкой интенсивности. Там, где интенсивность падающих на пластинку фотонов велика, после экспозиции появится темная область, а там, где интенсивность мала, - светлая. Если рассмотреть луч с очень малой интенсивностью, то очевидно, что мы не сможем точно указать, в какое место пластинки попадают фотоны. В наиболее темных местах пластинки вероятность попадания фотонов будет, конечно, наибольшей. [44]
Это уравнение показывает, что имеется определенная связь между плотностью частиц и квадратом волновой функции. Вероятностный характер такой системы легко продемонстрировать на примере рассмотрения дифракции светового луча при прохождении узкой щели. Если за щелью поместить фотографическую пластинку, то после необходимой экспозиции получается дифракционная картина, на которой будут видны темные и светлые области, соответствующие высокой и низкой интенсивности. Там, где интенсивность падающих на пластинку фотонов велика, после экспозиции появится темная область, а там, где интенсивность мала, - светлая. Если рассмотреть луч с очень малой интенсивностью, то очевидно, что мы не сможем точно указать, в какое место пластинки попадают фотоны. В наиболее темных местах пластинки вероятность попадания фотонов будет, конечно, наибольшей. Однако каждая область ограничена нерезко, что приводит к бесконечному множеству точек, в которых фотон мог бы удариться о пластинку. Итак, наши знания о местоположении фотона могут быть выражены с помощью вероятности, и мы приходим к заключению, что квадрат волновой функции выражает вероятность нахождения фотона в данном элементарном объеме. Безусловно, имеется аналогия между дифракцией светового луча и дифракцией пучка электронов. Можно было ожидать, что квантовая интерпретация, приемлемая для фотона, окажется применимой и для электрона. Поэтому можно постулировать, что квадрат волновой функции электрона пропорционален вероятности нахождения электрона в элементарном объеме dxdydz. Такое толкование - это просто постулат, который может оказаться соответствующим или несоответствующим действительности. До сих пор такая интерпретация, по-видимому, отвечает экспериментальным наблюдениям. Одним из наиболее значительных подтверждений применимости этого постулата является направленность связи в молекулах. [45]
Страницы: 1 2 3 4