Рассмотрение - возмущение
Cтраница 2
В случаях пространств с отличной от нуля кривизной и более сложной топологией качественно результат тот же - структура спектра зависит от топологии - но вид собственных функций сложнее, чем в простейших случаях. В качестве примера вспомним классическую работу Лифшица ( 1946), при рассмотрении возмущений в закрытой модели был получен дискретный спектр и найдена система собственных функций ( см. § 7 гл. [16]
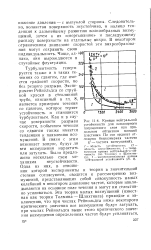 |
Кривые нейтральной устойчивости для ламинарного пограничного слоя при продольном обтекании плоской пластинки. По оси ординат отложена безразмерная частота ( f - частота возмущений. [17] |
В связи с этим возникает вопрос, будут ли эти возмущения нарастать или затухать. Было предложено несколько схем механизма неустойчивости. Одна из них, в отношении которой эксперименты степени согласуются, сводится к рассмотрению возмущений, представляющих собой совокупность малых колебаний в некотором диапазоне частот, которые накладываются на основное поле течения и могут им селективно усиливаться. [18]
Необходимо совместное решение системы кинетических уравнений, записанных для ионов и нейтральных частиц, возмущенных телом. Однако на высоте 200 км эти столкновения являются существенными и, как будет показано ниже, их вклад в формирование возмущения является определяющим. В связи с этим в данной работе основное внимание уделяется рассмотрению возмущения концентрации ионов нейтральными частицами, отраженными от тела, а также ионизации, производимой энергичными нейтральными частицами, отраженными от тела. [19]
Теория устойчивости упруго-пластических систем должна строиться на основе теории устойчивости движения. Должна рассматриваться не устойчивость какой-либо формы. Это не обязательно требует учета сил инерции. Если внешние силы консервативны, то в силу диссипативности упруго-пластической системы достаточным будет рассмотрение медленных возмущений. [20]
Ниже мы подробно останавливаемся на каждом типе возмущений. Лифшиц ( 1946) рассматривает также возмущения замкнутой ( Й1) и гиперболической ( й 1) Вселенной. Крайний случай возмущения мира как целого обсуждается в разделе IV. Мы продолжим рассмотрение возмущений в плоской модели. [21]
Это движение, обусловленное наличием электрического поля и градиента или кривизны магнитного поля, определяется спецификой лоренцовой силы. Для полноты нашего общего обзора движения частиц в магнитных полях необходимо рассмотреть еще движение вдоль силовых линий. В случае медленно меняющихся полей мощным средством исследования является метод адиабатических инвариантов. В небесной механике и в старой квантовой теории адиабатические инварианты использовались, с одной стороны, при рассмотрении возмущений движения, а с другой - для определения квантующихся величин. [22]
Страницы: 1 2