Проведенное рассмотрение

Cтраница 2

Проведенное рассмотрение отличается физической наглядностью и описывает принцип действия призмы в изломе широкого волновода. К сожалению, при этом основной вопрос об изменении амплитуды падающей волны остается открытым, и требуется дополнительное рассмотрение. Кроме того, полученные формулы неверно описывают переход к геометрической оптике ( ka Ф oo) t что довольно естественно, так как выражения (3.7.2), (3.7.4) для такого перехода теряют смысл. Действительно, если, например, на излом ( без призмы) падает плоская волна К Ф 0, то в правом волноводе уже не будет этой плоской волны, а ее энергия перейдет в волноводную ( паразитную) волну, соответствующую углу Брил-люэна, равному Ф, и возникает, кроме того, еще целый спектр других паразитных волн, обязанных своим появлением дифракции падающей волны на изломе. Аналогичное положение имеет место и при ka оо для призмы в прямолинейном волноводе. [16]

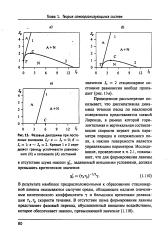Фазовые диаграммы при постоянных значениях /. а - I, 0. б - / 1. 0 - / 2. Кривые 1 и 2 определяют границу устойчивости равновесного ( N и потокового ( А состояний. [17]

Проведенное рассмотрение показывает, что диссипативная динамика течения песка по наклонной поверхности представляется схемой Лоренца, в рамках которой горизонтальная и вертикальная составляющие скорости играют роль параметра порядка и сопряженного поля, а наклон поверхности является управляющим параметром. [18]

Проведенное рассмотрение показывает, что диссипативная динамика самоорганизующейся системы может быть описана моделью Лоренца, в рамках которой вариация плотности ч играет роль внутреннего параметра, источник (1.165), сводящийся к энтропии s, представляет поле, сопряженное внутреннему параметру, а внутренняя энергия е является управляющим параметром. [19]

Проведенное рассмотрение указывает на иерархическую структуру картины отжига деформированных монокристаллов. Процессы, протекающие при деформации, ограничиваются третьим из указанных масштабов, тогда как отжиг связан с последним. [20]

Проведенное рассмотрение показывает, что в формулу для показателя преломления входят скорости распространения фаз световых волн, а не скорости распространения световых сигналов. [21]

Термодинамический потенциал и. [22]

Проведенное рассмотрение и полученные выше решения учитывают влияние на параметры доменных границ не только чисто электрических, но и упругих взаимодействий. [23]

Проведенное рассмотрение основывается на приближении идеального бездефектного материала. [24]

Спектр собственных колебаний в плазме с монотонным. [25]

Проведенное рассмотрение показывает, что вывод об отсутствии собственных колебаний, полученный с помощью идеального уравнения (9.2), свидетельствует о недостаточности приближения идеальной плазмы. В реальной плазме существуют приграничные затухающие собственные колебания, как бы ни была велика ее проводимость. Рост проводимости вызывает лишь сгущение спектра. [26]

Проведенное рассмотрение показывает, что возможность использования правила обхода Ландау при решении волнового уравнения свидетельствует об отборе энергии колебаний в окрестности резонансной точки. При однородном распределении температуры энергия диссипирует в результате ион-электронных столкновений. Если распределение температуры неоднородно, то колебаний в окрестности резонансной точки трансформируются в более коротковолновые. Последние поглощаются под действием ион-ионных столкновений в окрестности точки, в которой фазовая скорость колебаний совпадает со скоростью ларморовского дрейфа, рассчитанной в предположении однородности температуры. Обычно в высокотемпературной ( термоядерной) плазме частоты кулоновских столкновений малы по сравнению с другими характерными частотами, однако влияние столкновений усиливается с уменьшением пространственного масштаба явления. В областях, где происходит поглощение колебаний, масштаб резко сокращается, и именно поэтому столкновительное поглощение оказывается конечным, даже если частоту столкновений формально устремить к нулю. Столкновения переводят энергию колебаний в тепловую. [27]

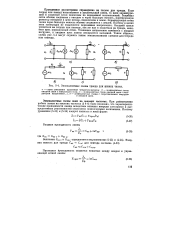Эквивалентные схемы триода для низких частот. [28]

Проведенное рассмотрение справедливо не только для триода. Если тетрод или пентод используется в усилительной схеме, то цепи экранирующей и защитной сеток заземлены по переменной составляющей. Защитная сетка обычно соединена с катодом и через большую емкость, шунтирующую резистор смещения в цепи катода, подключена к земле. Экранирующая сетка также через большую емкость обычно соединяется с землей. Поэтому в цепях этих электродов не выделяются переменные напряжения. Входной цепью усилителя на тетроде или пентоде, так же как и усилителя на триоде, является цепь управляющей сетки. Усиленное напряжение снимается с анодной нагрузки, и анодная цепь лампы оказывается выходной. Таким образом, схемы рис. 5 - 4 могут служить также эквивалентными схемами для тетрода или пентода. [29]

Проведенное рассмотрение относится к случаю непрерывного СВЧ сигнала. При воздействии коротких импульсов мощности диодная структура не успевает разогреваться до температуры, соответствующей данному уровню мощности. Поэтому максимальная мощность расимп, которую может поглощать диод в течение короткого отрезка времени, будет больше величины Ррасмакс, причем разница будет тем больше, чем короче импульсы. Для полного описания свойств диода необходимо указывать зависимость Рраоимп от длительности импульса. Очевидно, РраСимп зависит также от температуры корпуса диода. [30]

Страницы: 1 2 3 4 5