Модельное рассмотрение

Cтраница 1

Модельное рассмотрение показывает [11], что катенаны могут образоваться уже из цепочек с 20 - 30 атомами углерода. Отметим, что структуры А, Б, Д и Е проявляют хиральность. [1]

Модельное рассмотрение задачи о температурной зависимости модуля сдвига в рамках метода молекулярной динамики [1239] показало, что низкочастотный модуль сдвига медленно уменьшается с ростом температуры вплоть до Т 0 9 Тт, а затем резко падает при приближении к Тт за счет нелинейных фононных взаимодействий. [2]

Основной результат модельного рассмотрения комп-тои-эффекта, приведенного здесь, состоит в том, что амплитуда этого процесса обладает аномальными свойствами с точки зрения гипотезы гладкости. [3]

Поворотно-изомерное рассмотрение является модельным рассмотрением цепи с непрерывным распределением вероятностей для ориентации звеньев. Поворотно-изомерная цепь в смысле теории вероятностей не является чем-либо принципиально новым но сравнению с цепью, в которой имеются фиксированные валентные углы и свободное вращение. В свою очередь, как показано в § 25, такая цепь может быть адекватно представлена свободно-сочлененной цепью, иными словами, в ней нет дальнего порядка. Отекла следует, что асимптотическое распределение длин поворотно-изомерной цепи также должно быть Гауссовым. То же, как это доказывается в теории вероятностей, имеет место для асимптотического поведения суммы большого числа переменных, связанных в регулярную цепь Маркова. [4]

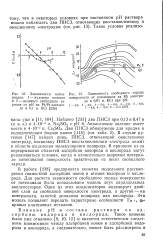Зависимости потен - Р.ис. 13. Зависимость свободного заряда. [5]

В работе [238] предпринята попытка модельного рассмотрения совместной адсорбции ионов и атомов водорода и кислорода. Для расчета зависимости свободного заряда поверхности от потенциала была использована модель двух параллельных конденсаторов. Один из этих конденсаторов моделирует двойной слой на свободной поверхности электрода, а другой - на поверхности, занятой диполями водорода или кислорода. Эта модель позволяет передать характерные особенности Гн, РГ-кривых платиновых металлов. [6]

В этой и следующей главах приведено модельное рассмотрение характерных для биологии колебательных, регуляторных и эволюционных процессов. Основным методом является исследование кинетических уравнений, описывающих модель, но в ряде случаев такое исследование должно быть дополнено решением соответствующих стохастических задач. [7]

Так как раскрытия трещин в горных породах на глубинах залегания нефтегазоносных пластов не превышают 10 - 2 см, то при модельном рассмотрении движения жидкости на участке трещины между линиями пересечения последней с другими трещинами можно пренебрегать концевыми эффектами. [8]

Информационное обеспечение опирается, с одной стороны, на прямые измерения значений параметров задачи и на статистические выводы, сделанные на основании таких измерений, а с другой - на модельные рассмотрения, согласно которым значение параметра получается как решение некоторой задачи. Переход от постановки прикладных задач к их решению требует привлечения дальнейших аспектов математического обеспечения. [9]

Первая была посвящена модельному рассмотрению различных задач квантовой механики и квантовой электродинамики и методам оценок физических величин. Здесь мы с изумлением узнавали, что формулу Резерфорда для рассеяния на малые углы или величину лэм-бовского сдвига можно получить путем простых рассуждений и не проделывая сложных расчетов, с которыми мы уже были знакомы из других курсов. [10]

Относительно степенного показателя функции V ( l), на основе данных разных авторов для широкой гаммы горных пород в обобщенном виде можно заключить: показатель степени всегда ниже кубической, уменьшается с ростом электрической прочности горных пород и степени их неоднородности, с увеличением разрядного промежутка и уменьшением крутизны фронта импульса напряжения. Это отражает объясненное выше отличие реального развития процесса в электродной конструкции от модельного рассмотрения со статической картиной электрического поля в промежутке. [11]

Сферические аппараты реже встречаются в химической технологии: это обычно резервуары для жидкостей и газов; нередко их изолируют в тепловом отношении - тогда речь идет о многослойных сферических стенках. Кроме того, анализ кондуктивного теплопереноса через сферические стенки оказывается полезным при модельном рассмотрении некоторых случаев конвективного теплопереноса ( см. разд. [12]

В самом деле, для поверхностно-активных органических веществ расчет по уравнению (2.22) всегда дает значения ГЛ 0 в области адсорбции и ГА 0 в области, где произошла десорбция органического вещества. Второй аргумент, указывающий на то, что величина, определяемая по формуле (2.22), близка по физическому смыслу к поверхностной концентрации, вытекает кз модельного рассмотрения адсорбционного слоя. [13]

Предполагаем, что источник колебаний давления представляет собой сферу радиуса R, а жидкость со взвешенными в ней частицами окружает источник со всех сторон и занимает неограниченное пространство. Внешними силами и внутренней диссипацией в жидкости, как и в предыдущей задаче, а также действием внешних массовых сил пренебрегаем. Таким образом, данное модельное рассмотрение справедливо лишь на небольших расстояниях от источника, когда затуханием волны можно пренебречь. Вводим сферическую систему координат с началом в центре источника колебаний давления. [14]

Сначала рассмотрим случай плоской бегущей волны, распространяющейся в неограниченном пространстве в горизонтальном направлении. Внешними силами и внутренней диссипацией в жидкости пренебрегаем. Таким образом, данное модельное рассмотрение справедливо лишь на небольших расстояниях от источника, когда затуханием волны можно пренебречь. [15]

Страницы: 1